Analysis Of Algorithms

Analysis Of Algorithm

Interview Questions: Analysis of Algorithms (ungraded)

1. 3-SUM in quadratic time.

Design an algorithm for the 3-SUM problem that takes time proportional to $n^2$ in the worst case. You may assume that you can sort the $n$ integers in time proportional to $n^2$ or better.

Note: these interview questions are ungraded and purely for your own enrichment. To get a hint, submit a solution.

Solution

在课程中已经给出了两个求解 3-SUM 问题的算法：暴力方法 ThreeSum 和改进算法 ThreeSumFast。

其中暴力方法 ThreeSum 的时间复杂度为 $O(N^3)$，改进算法 ThreeSumFast 的时间复杂度为 $O(N^2logN)$。

题目要求我们再实现一种求解 3-SUM 问题的算法 ThreeSumQuadratic，要求其时间复杂度为 $O(N^2)$。

分析 ThreeSumFast，虽然其对数组 a 进行排序，但排序后，仍然需要对一堆二元整数组 (a[i], a[j]) 做关于其和的负数 -(a[i]+a[j]) 的 BinarySearch，这堆二元整数组有 $\sim\frac{1}{2}N^2$ 多个，这意味着我们要做 $\sim \frac{1}{2}N^2$ 次 BinarySearch。

Note：

我们说时间复杂度一般是指 Big-Oh：$O$。

排序的时间复杂度可以是 $O(NlogN)$ 也可以是 $O(N^2)$，取决于排序算法。但显然，在 FastThreeSum 中，在一堆二元组上做 BinarySearch 才是主要操作。

我们需要摆脱二元整数组，否则时间复杂度不可能降低到 $O(N^2)$，方法如下：

package analysis_of_algs;

import java.util.Arrays;

import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;
import edu.princeton.cs.algs4.Stopwatch;

public class ThreeSumQuadratic {
    
    public static int count(int[] a) {
        Arrays.sort(a);
        int N = a.length;
        int count = 0;
        
        for (int i = 0; i < N - 2; i++) {
            int j = i + 1;
            int k = N - 1;
            
            while (j < k) {
                int sum = a[i] + a[j] + a[k];
                if (sum < 0) {
                    j++;
                }
                else if (sum > 0) {
                    k--;
                }
                else {
                    count++;
                    j++;
                }
            }

        }
        
        return count;
    }

    public static void main(String[] args) {
        int[] a = new In(args[0]).readAllInts();
        Stopwatch stopwatch = new Stopwatch();
        StdOut.println(count(a));
        double time = stopwatch.elapsedTime();
        StdOut.println(time);
    }
    
}

只要排序算法的时间复杂度低于 $O(N^2)$，以上代码的方法即满足需求。

效果对比（ThreeSumFast 和 ThreeSumQuadratic 使用相同的排序算法）：

2. Search in a bitonic array.

An array is bitonic (双调) if it is comprised of an increasing sequence of integers followed immediately by a decreasing sequence of integers. Write a program that, given a bitonic array of $n$ distinct integer values, determines whether a given integer is in the array.

• Standard version: Use $\sim 3\lg n$ compares in the worst case.
• Signing bonus: Use $\sim 2\lg n$ compares in the worst case (and prove that no algorithm can guarantee to perform fewer than $\sim 2\lg n$ compares in the worst case).

Solution

这里将列出三种算法。

• 首先是我想到的算法（算法一 BitonicSearch），我想当然地以为算法一是 $\sim2\lg n$ 的，实际上，算法一的性能是最差的，其时间复杂度为 $O(\lg^2N)$。思路如下：

  • 寻找数组的中间点 mid

  • 确定 a[mid] 附近的排序情况，是降序还是升序（等价于确定最大值是在 a[mid] 的左边还是右边）

  • 确定 key 与 a[mid] 的大小情况

  • 如果是降序，那么显然 a[mid]~a[hi] 都是降序，此时：

    • 若 key 比 a[mid] 要小，那么 key 可能在 a[mid]~a[hi] 中，也可能在 a[lo]~a[mid] 中。

      对于 a[mid]~a[hi]，其为降序数组，使用 BinarySearch，找到则返回，否则再到 a[lo]~a[mid] 中寻找，显然 a[lo]~a[mid] 是一个更小的双调数组，可递归求解。

    • 若 key 比 a[mid] 要大，那么 key 只可能在 a[lo]~a[mid] 中，可递归求解。

  • 如果是升序，那么显然 a[lo]~a[mid] 都是升序，此时：

    • 若 key 比 a[mid] 要小，那么 key 可能在 a[lo]~a[mid] 中，也可能在 a[mid]~a[hi] 中。

      对于 a[lo]~a[mid]，其为升序数组，使用 BinarySearch，找到则返回，否则再到 a[mid]~a[hi] 中寻找，显然 a[mid]~a[hi] 是一个更小的双调数组，可递归求解。

    • 若 key 比 a[mid] 要大，那么 key 只可能在 a[mid]~a[hi] 中，可递归求解。

  网上🏄 发现，其实也有很多人和我一样把算法一想当然地认为是 $\sim2\lg N$ 的，对于其时间复杂度为 $O(\lg^2N)$ 的解释参考：Given a bitonic array and element x in the array, find the index of x in 2log(n) time - StackOverflow。代码如下：

  package analysis_of_algs;
  
  import edu.princeton.cs.algs4.StdOut;
  
  public class BitonicSearch {
      
      private static int leftBinarySearch(int[] a, int key, int lo, int hi) {
          while (lo <= hi) {
              int mid = lo + (hi - lo) / 2 ;
              if (key < a[mid]) hi = mid - 1;
              else if (key > a[mid]) lo = mid + 1;
              else return mid;
          }
          return -1;
      }
      
      private static int rightBinarySearch(int[] a, int key, int lo, int hi) {
          while (lo <= hi) {
              int mid = lo + (hi - lo) / 2;
              if (key > a[mid]) hi = mid - 1;
              else if (key < a[mid]) lo = mid + 1;
              else return mid;
          }
          return -1;
      }
      
      public static int find(int[] a, int key) {
          return find(a, key, 0, a.length-1);
      }
      
      private static int find(int[] a, int key, int lo, int hi) {
          
          if (lo > hi) return -1;
          int mid = lo + (hi - lo) / 2;
          if (a[mid] == key) return mid;
          
          int rbResult = 0;
          int lbResult = 0;
          
          // if a[mid] nearby is descending order
          if (a[mid] > a[mid+1]) {
              // if a[mid] > key, rightBinarySearch on a[mid+1]~a[hi]  
              if (a[mid] > key) {
                  rbResult = rightBinarySearch(a, key, mid+1, hi);
                  // if rightBinarySearch not find, then key also may on a[lo]~a[mid-1]
                  if (rbResult == -1) {
                      return find(a, key, lo, mid-1);
                  } 
                  else return rbResult;
              }
              // else a[mid] < key, then key only possible on a[lo]~a[mid-1]
              else {
                  return find(a, key, lo, mid-1);
              }
          }
          // else a[mid] nearby is ascending order
          else {
              // if a[mid] > key, leftBinarySearch on a[lo]~a[mid-1]
              if (a[mid] > key) {
                  lbResult = leftBinarySearch(a, key, lo, mid-1);
                  // if leftBinarySearch not find, then key also may on a[mid+1]~a[hi]
                  if (lbResult == -1) {
                      return find(a, key, mid+1, hi);
                  }
                  else return lbResult;
              }
              // else a[mid] < key, then key only possible on a[mid+1]~a[hi]
              else {
                  return find(a, key, mid+1, hi);
              }
          }
      }
  
      public static void main(String[] args) {
          
          int[] a = {1, 2, 3, 4, 5, 6, 29, 28, 27, 23, 22, 19, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7};
          
          for (int i = 0; i < 31; i++) {
              int ret = find(a, i);
              StdOut.println(i + " : " + (ret == -1 ? "not find" : "find at " + ret));
          }
          
      }
      
  }

• 其次是算法二 BitonicSearchStd，也即题目中要求的 Standard version，$\sim 3\lg N$ 的比较数。

  算法二的思想很简单，先采用 BinarySearch 的变式把最大值给找到，这在 worst case 下是 $\sim \lg N$ 的比较数，然后对最大值的左半边和右半边分别使用 BinarySearch，左右各有 $2\lg \frac{N}{2}=\lg N-2=\sim\lg N$ 的比较数，故总共有 $\sim 3\lg N$ 的比较数。

  代码如下：

  package analysis_of_algs;
  
  import edu.princeton.cs.algs4.StdOut;
  
  public class BitonicSearchStd {
      
      private static int leftBinarySearch(int[] a, int key, int lo, int hi) {
          while (lo <= hi) {
              int mid = lo + (hi - lo) / 2 ;
              if (key < a[mid]) hi = mid - 1;
              else if (key > a[mid]) lo = mid + 1;
              else return mid;
          }
          return -1;
      }
      
      private static int rightBinarySearch(int[] a, int key, int lo, int hi) {
          while (lo <= hi) {
              int mid = lo + (hi - lo) / 2;
              if (key > a[mid]) hi = mid - 1;
              else if (key < a[mid]) lo = mid + 1;
              else return mid;
          }
          return -1;
      }
      
      private static int findMaxIndex(int[] a) {
          int lo = 0;
          int hi = a.length - 1;
          while (lo < hi) {
              int mid = lo + (hi - lo) / 2;
              if (a[mid] > a[mid+1]) {
                  hi = mid;
              } else {
                  lo = mid + 1;
              }
          }
          return hi;
      }
      
      public static int find(int[] a, int key) {
          int lo = 0;
          int hi = a.length - 1;
          int maxIndex = findMaxIndex(a);
          
          if (key == a[maxIndex]) return maxIndex;
          
          int lbResult = leftBinarySearch(a, key, lo, maxIndex - 1);
          if (lbResult != -1) return lbResult;
          
          int rbResult = rightBinarySearch(a, key, maxIndex + 1, hi);
          if (rbResult != -1) return rbResult;
          
          return -1;
      }
      
      public static void main(String[] args) {
          
          int[] a = {1, 2, 3, 4, 5, 6, 29, 28, 27, 23, 22, 19, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7};
          
          for (int i = 0; i < 31; i++) {
              int ret = find(a, i);
              StdOut.println(i + " : " + (ret == -1 ? "not find" : "find at " + ret));
          }
          
      }
      
  }

Note：

算法一和算法二中使用的 leftBinarySearch 和 rightBinarySearch 都是课程中所说的 “3-way compare” 实现，也即有 2 次比较，程序流有 3 路分支。所以，算法二中对左右半边进行 BinarySearch 比较数为 $2\lg \frac{N}{2}$ 而非 $\lg\frac{N}{2}$。在算法三中，将给出 “2-way compare” 实现 leftSearch 和 rightSearch（一般我们还是会用更加直观的 “3-way compare”）。

此外，我们在查看 a[mid] 附近的情况时，一般用 a[mid+1] 而非 a[mid-1]，因为在 while(lo < hi) 的前提下，a[mid+1] 总是存在的，而 a[mid-1] 我们需要额外检查 mid-1 下标的合法性。

• 最后是算法三 BitonicSearchBonus，也即题目中要求的 bonus，$\sim 2\lg N$ 的比较数。

  综合算法一和算法三，容易想到去掉寻找最大值的过程。

  事实上，算法三和算法一只有一个关键的地方有不同，就 a[mid] 附近是降序的情况而言，算法一是：

  若 key 比 a[mid] 要小，那么 key 可能在 a[mid]~a[hi] 中，也可能在 a[lo]~a[mid] 中。

  对于 a[mid]~a[hi]，其为降序数组，使用 BinarySearch，找到则返回，否则再到 a[lo]~a[mid] 中寻找，显然 a[lo]~a[mid] 是一个更小的双调数组，可递归求解。

  关键的地方就在后者，a[lo]~a[mid] 我们知道是一个相对更小的双调数组（对应下图中的蓝色和黑色部分），故在算法一中，我们将其视为子问题递归求解。

  而实际上，当 key < a[mid] 时（也即要寻找的 key 值位于蓝色部分时），我们可以直接在 a[lo]~a[mid] 这个双调数组上使用 BinarySearch 并得到正确的结果 。

  这就是算法三的关键思想：对于一个双调数组，如果你要寻找的 key 值位于 a[lo] 和 a[hi] 之间，那么直接使用 BinarySearch 是正确的。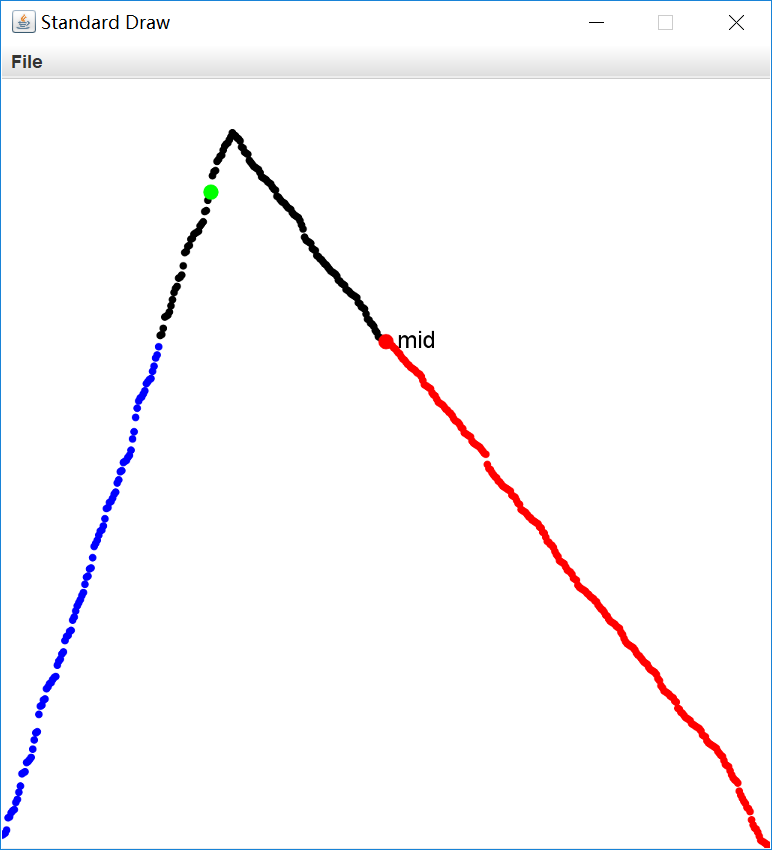

  

  好了，对于 key < a[mid] 的情况，key 在两边都有可能存在（蓝色和红色部分），我们直接对两边进行 BinarySearch 就好了，即使其中一边是双调数组，此时有 $\sim 2\lg N$ 的比较数。

  那对于 key > a[mid] 的情况，key 处于黑色部分，我们只需要根据 a[mid] 附近的情况进行范围缩小即可。比如若我们要找到 key 是上图中的绿点，由于 a[mid] 附近是降序（说明 key 位于 mid 的左边），显然此时 key 只可能存在于左边 a[lo]~a[mid]，此时令 hi=mid-1 。依次类推，不断重复地缩小范围，使转换到 key < a[mid] 的情况，然后就能对两边 BinarySearch 进行求解。

  如果要寻找的 key 特别大（比数组中的所有元素都大），那么此时有 $\sim \lg N$ 的比较数。一般地，假设 k 次缩小范围，则有：$k+2\lg \frac{N}{2^{k+1}}=k+2(\lg N - (k+1))=2\lg N-k-2=\sim 2\lg N$。

  对于双调数组查找问题，理想地，如果直接提供最大值下标，此时对最大值两边分别进行 BinarySearch 也需要 $\sim2\lg N$ 的比较数，所以算法三应该已经相当好了，至于题目中要求证明算法三是最优的（没有算法能做到少于 $\sim2\lg N$ 的比较数），这我就不知道了…

  代码如下（注意其中 BinarySearch 的 “2-way compare” 实现）：

  package analysis_of_algs;
  
  import edu.princeton.cs.algs4.StdOut;
  
  public class BitonicSearchBonus {
  
      private static int leftSearch(int[] a, int key, int lo, int hi) {
          while (lo < hi) {
              int mid = lo + (hi - lo) / 2;
              if (key <= a[mid]) {
                  hi = mid;
              }
              else {
                  lo = mid + 1;
              }
          }
          if (key == a[lo]) return lo;
          else return -1;
      }
      
      private static int rightSearch(int[] a, int key, int lo, int hi) {
          while (lo < hi) {
              int mid = lo + (hi - lo) / 2;
              if (key >= a[mid]) {
                  hi = mid;
              }
              else {
                  lo = mid + 1;
              }
          }
          if (key == a[lo]) return lo;
          else return -1;
      }
      
      public static int find(int[] a, int key) {
          int lo = 0;
          int hi = a.length - 1;
          while (lo < hi) {
              int mid = lo + (hi - lo) / 2;
              if (key == a[mid]) return mid;
              if (key < a[mid]) {
                  int lbResult = leftSearch(a, key, lo, mid);
                  if (lbResult != -1) {
                      return lbResult;
                  } 
                  else return rightSearch(a, key, mid, hi);
              }
              else {
                  if (a[mid] < a[mid+1]) {
                      lo = mid + 1;
                  } 
                  else {
                      hi = mid - 1;
                  }
              }
          }
          return -1;
      }
      
      public static void main(String[] args) {
          
          int[] a = {1, 2, 3, 4, 5, 6, 29, 28, 27, 23, 22, 19, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7};
          
          for (int i = 0; i < 31; i++) {
              int ret = find(a, i);
              StdOut.println(i + " : " + (ret == -1 ? "not find" : "find at " + ret));
          }
          
      }
  }

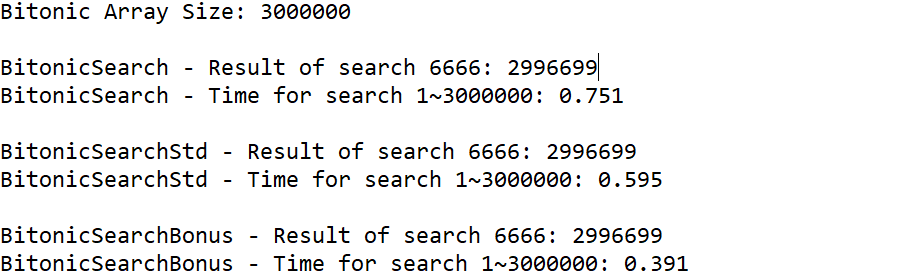
效果对比

3. Egg drop.

Suppose that you have an $n$-story building (with floors $1$ through $n$) and plenty of eggs. An egg breaks if it is dropped from floor $T$ or higher and does not break otherwise. Your goal is to devise a strategy to determine the value of $T$ given the following limitations on the number of eggs and tosses:

• Version 0: $1$ egg, $\le T$ tosses.
• Version 1: $\sim1\lg n$ eggs and $\sim1\lg n$ tosses.
• Version 2: $\sim\lg T$ eggs and $\sim2\lg T$ tosses.
• Version 3: $2$ eggs and $\sim2\sqrt{n}$ tosses.
• Version 4: $2$ eggs and $\le c \sqrt T$ tosses for some fixed constant $c$.

Solution

题意：假设有一栋 $n$ 层高的建筑，已知在层数 $T$ 或更高层投掷鸡蛋鸡蛋会碎掉，现在提供有限的鸡蛋且仅允许你投掷有限次数，要求你找到这个 $T$ 值。

• Version 0: $1$ egg, $\le T$ tosses.

  仅提供 $1$ 个鸡蛋，那我们要确保在精确得到 $T$ 之前，鸡蛋不能碎。

  我们拿着这 $1$ 个鸡蛋从 $1$ 楼到 $n$ 楼依次投掷一次，到 $T$ 楼则会碎掉，从而在 $\le T$ 次投掷下使用 $1$ 个鸡蛋得到结果。

• Version 1: $\sim1\lg n$ eggs and $\sim1\lg n$ tosses.

  采用二分查找的思想，首先在 $n/2$ 层投掷：

  • 如果鸡蛋碎了，说明 $T < n/2$， 我们在 $[1,\ n/2)$ 层再进行查找（后续在 $n/4$ 层投掷）
  • 如果鸡蛋没碎，说明 $T>n/2$，我们在 $(n/2,\ n]$ 层再进行查找（后续在 $n/2+n/4$ 层投掷）

  本质上就是二分查找，虽然不知道 $T$ 具体是什么，但是鸡蛋是否破碎能够提供一种比较来支持二分查找，二分次数 $\sim\lg n$ 也即投掷次数，消耗鸡蛋数理论上肯定要比投掷次数要少，故满足题目要求。

• Version 2: $\sim\lg T$ eggs and $\sim2\lg T$ tosses.

  我们按照 $1,2,4,8,16,32,\cdots,2^k$ 的楼层顺序进行投掷，只要鸡蛋不碎，就将楼层翻倍再进行投掷。

  假设鸡蛋在 $2^u$ 碎了，那么显然有 $2^{u-1}\lt T\le 2^u$。 此时我们已经进行了 $u=\sim \lg T$ 次投掷，鸡蛋就碎了 $1$ 个。然后我们在 $(2^{u-1},2^u]$ 上进行二分查找，这又要进行 $\sim \lg T$ 次投掷，消耗鸡蛋数理论上小于 $\sim\lg T$。两步操作加起来即消耗 $\sim \lg T$ 个鸡蛋，进行 $\sim 2\lg T$ 次投掷。

• Version 3: $2$ eggs and $\sim2\sqrt{n}$ tosses.

  我们按照 $\sqrt{n},2\sqrt{n},3\sqrt{n},\cdots,k\sqrt{n}$ 的楼层顺序进行投掷。

  假设第一个鸡蛋在 $u\sqrt{n}$ 处投掷时破碎了，那么显然 $(u-1)\sqrt{n}\lt T\le u\sqrt{n}$，在 worst case 下我们已经进行了 $\sim \sqrt{n}$ 次投掷了。然后我们在 $((u-1)\sqrt{n},u\sqrt{n}]$ 上从小到大顺序进行尝试，直到第二个鸡蛋破碎，这又要进行 $\sim \sqrt{n}$ 次投掷。两步操作加起来即消耗 $2$ 个鸡蛋，进行 $\sim 2\sqrt{n}$ 次投掷。

  按提示，还能再改进到 $\sim \sqrt{2n}$ tosses，这在文章 The Two Egg Problem - DataGenetics 中的 Minimization of Maximum Regret 以及 Two egg solution 部分已经讲得非常清楚了，此处不再多做叙述。

• Version 4: $2$ eggs and $\le c \sqrt T$ tosses for some fixed constant $c$.

  我们按照 $1,3,6,10,15,21,\cdots,\frac{k(k+1)}{2}$ 的楼层顺序进行投掷。

  假设第一个鸡蛋在 $\frac{u(u+1)}{2}$ 处投掷时破碎了，那么显然 $\frac{(u-1)u}{2}\lt T\le \frac{u(u+1)}{2}$，令 $T\le \frac{u(u+1)}{2}$ 可知 $u=\sim\sqrt{2T}$，故第一个鸡蛋破碎时我们进行了 $\sim \sqrt{2T}$ 次投掷。然后在 $(\frac{(u-1)u}{2}, \frac{u(u+1)}{2}]$ 上从小到大顺序进行尝试，直到第二个鸡蛋破碎，这又要进行至多 $\frac{u(u+1)}{2}-\frac{(u-1)u}{2}=u=\sim \sqrt{2T}$ 次投掷。两步操作加起来即消耗 $2$ 个鸡蛋，进行 $\sim 2\sqrt{2T}$ 次投掷，也即 $c=2\sqrt{2}$。

参考

• Given a bitonic array and element x in the array, find the index of x in 2log(n) time - StackOverflow
• Egg drop problem - StackExchange
• The Two Egg Problem - DataGenetics