Lec21 - 特征值和特征向量

第 21 课 特征值和特征向量

特征值与特征向量初探

给定矩阵 $A$ ，矩阵 $A$ 乘以向量 $x$，就像是使用矩阵 $A$ 作用在向量 $x$上，最后得到新的向量 $Ax$。在这里，矩阵 $A$ 就像是一个函数，接受一个向量 $x$ 作为输入，给出向量 $Ax$ 作为输出。

在这一过程中，我们对一些特殊的向量很感兴趣，也即 $x$ 和 $Ax$ 始终保持同一个方向，这是比较特殊的，因为在大多情况下，$Ax$ 与 $x$ 指向不同的方向。

在这种特殊的情况下，$Ax$ 平行于 $x$，我们把满足这个条件的非零向量 $x$ 称为 $A$ 特征向量，而 $\lambda$ 为 $A$ 的特征值 。这个平行条件用方程表示就是：

$$\displaylines{ Ax=\lambda x }$$

对这个式子，我们试着计算特征值为 $0$ 的特征向量，易得 $Ax=0x=0$，因此，特征值为 $0$ 的特征向量位于 $A$ 的零空间中。

显然对于奇异矩阵（不可逆），必然存在非零向量使得 $Ax=0$，所以若矩阵是奇异的，那么它有一个特征值为 $\lambda =0$。

• 我们先来看投影矩阵 $P=A(A^TA)^{-1}A^T$ 的特征值和特征向量。

  

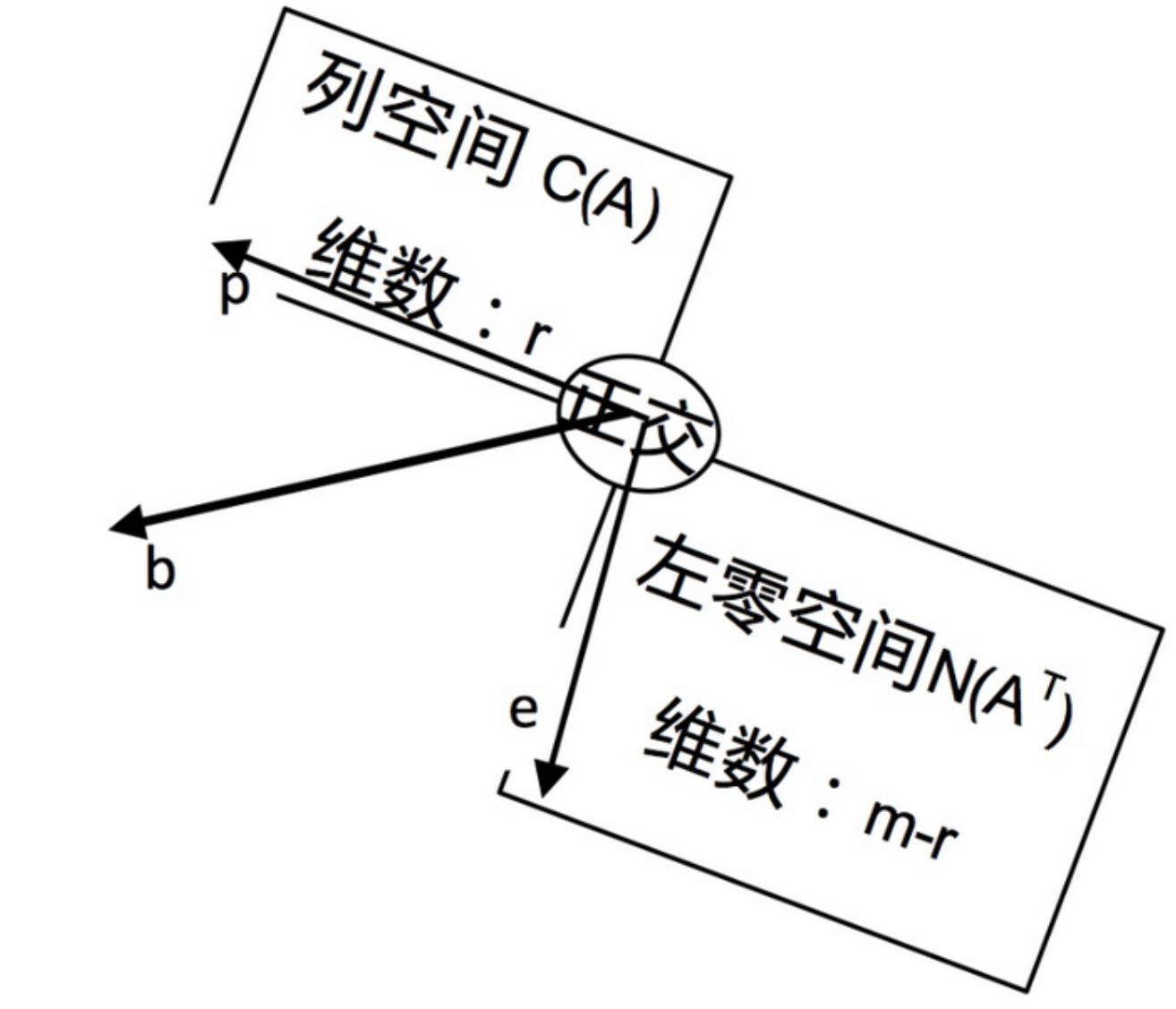
  • 用向量 $b$ 乘以投影矩阵 $P$ 得到投影向量 $Pb$，在这个过程中，只有当 $b$ 本身已经处于投影平面（即 $A$ 的列空间）中时，$Pb$ 才可能与 $b$ 是同向的，此时 $b$ 投影前后完全相同（$Pb=1\cdot b$）。因此，投影平面（$A$ 的列空间）中的所有向量都是投影矩阵的特征向量，且它们的特征值为 $1$。
  • 再来观察投影平面的法向量，也即向量 $e$ 。既然向量 $e$ 与投影平面垂直，那么必然有 $Pe=0$，任何向量都与 $0$ 向量是同向的。因此，投影平面的所有法向量（$A$ 的左零空间）也同样是投影矩阵的特征向量，且它们的特征值为 $0$。

  综上可知，投影矩阵 $P=A(A^TA)^{-1}A^T$ 的特征值为 $\lambda=1,0$。

• 再看另外一个例子，二阶置换矩阵 $A=\begin{bmatrix}0& 1\\1& 0\end{bmatrix}$，经过这个矩阵处理的二维向量 $x$，其元素会互相交换，即：$\begin{bmatrix}x_1\\x_2\end{bmatrix}$ 会变为 $\begin{bmatrix}x_2\\x_1\end{bmatrix}$。若交换后的 $\begin{bmatrix}x_2\\x_1\end{bmatrix}$ 是初始向量 $\begin{bmatrix}x_1\\x_2\end{bmatrix}$ 与一个因子的乘积，那么根据特征值和特征向量的定义可知：

  • $A$ 有特征值为 $1$ 的特征向量（即经过矩阵交换元素前后仍然不变），型为 $\begin{bmatrix}1\\1\end{bmatrix}$。
  • $A$ 有特征值为 $-1$ 的特征向量（即经过矩阵交换元素前后方向相反），型为 $\begin{bmatrix}1\-1\end{bmatrix}$。

  就此例，我们提前说一些特征值的性质：

  • 一个 $n\times n$ 的矩阵包含 $n$ 个特征值（可能其中有一些特征值的值相同，甚至有些特征值非实数），而这些特征值的和与该矩阵对角线元素的和相同（$\sum_{i=1}^n \lambda_i=\sum_{i=1}^n a_{ii}$），我们把矩阵对角线元素之和称为矩阵的迹。

    在上面二阶转置矩阵的例子中，如果我们求得了一个特征值 $1$，那么利用迹的性质，我们就可以直接推出另一个特征值是 $-1$。这条性质我们将在本课后面给予证明。

  • 对称矩阵，其特征向量互相垂直。

    矩阵越特殊，则我们得到的特征值与特征向量也就越特殊。看上面的二阶置换矩阵中，因为它是一个对称矩阵，所以其特征值为实数：$1,−1$，而且它们的特征向量是正交的。

    证明：对称矩阵的特征向量正交。

    $$\displaylines{ 设\ \lambda_1\ 和\ \lambda_2\ 是对称矩阵\ A\ 的两个不同的特征值，对应的特征向量分别为\ x_1\ 和\ x_2\\ \therefore Ax_1=\lambda_1x_1,\ Ax_2=\lambda_2x_2\\ 对\ Ax_1=\lambda_1x_1\ 左乘\ x_2^T\ 得：\quad x_2^TAx_1=\lambda_1x^T_2x_1\qquad\\ x^T_2Ax_1=(Ax_2)^Tx_1=(\lambda_2x_2)^Tx_1=\lambda_2x^T_2x_1=\lambda_1x^T_2x_1\\ 也即\ (\lambda_1-\lambda_2)x^T_2x_1=0\\ 又\because \lambda_1\ne\lambda_2\ \\\therefore x^T_2x_1=0\\ \therefore 对称矩阵的特征向量正交。 }$$

---

求解特征值和特征向量：$Ax=\lambda x$

对于方程 $Ax=\lambda x$ ，有两个未知数，我们需要利用一些技巧从这一个方程中一次解出两个未知数（一个是特征值一个是特征向量），首先移项得 $(A-\lambda I)x=0$。

观察新方程 $(A-\lambda I)x=0$，右边的矩阵 $\lambda I$ 相当于将 $A$ 矩阵平移了 $\lambda$ 个单位，而如果新方程有非零解 $x$（因为要求特征向量不可为零向量），则这个平移后的矩阵 $(A-\lambda I)$ 一定是奇异矩阵。

我们现在想要求的特征向量正是 $(A-\lambda I)x=0$ 的非零解 $x$，这就需要 $(A-\lambda I)$ 为奇异矩阵，结合行列式可得：

$$\displaylines{ \det(A-\lambda I) =0 }$$

这样一来，方程中就没有 $x$ 了，$\det(A-\lambda I) =0$ 也叫作特征方程。求解特征方程的带特征值 $\lambda$，代回 $(A-\lambda I)x=0$，继续求 $(A-\lambda I)$ 的零空间即可。

• 举一个简单的例子，求解 $A=\begin{bmatrix}3& 1\\1& 3\end{bmatrix}$ 的特征值与相应的特征向量。

  首先计算 $\det{(A-\lambda{I})}=\begin{vmatrix}3-\lambda& 1\\1& 3-\lambda\end{vmatrix}=0$，由二阶行列式公式可得：$(3-\lambda)^2-1=\lambda^2-6\lambda+8=0$，求得 $\lambda_1=4,\lambda_2=2$。可以看到一次项系数 $-6$ 和矩阵的迹 $3+3$ 有关，此外，常数项 $8$ 与矩阵的行列式有关。至于为什么，我们将在后面给予解释。

  继续计算特征向量，$A-4I=\begin{bmatrix}-1& 1\\1& -1\end{bmatrix}$，显然矩阵是奇异的（如果是非奇异说明特征值计算有误），解出 $\lambda_1$ 对应的一个特征向量 $x_1=\begin{bmatrix}1\\1\end{bmatrix}$；同理计算另一个特征向量，$A-2I=\begin{bmatrix}1& 1\\1& 1\end{bmatrix}$，解出 $\lambda_2$ 对应的一个特征向量 $x_2=\begin{bmatrix}1\-1\end{bmatrix}$。

  回顾前面转置矩阵的例子，对矩阵 $A’=\begin{bmatrix}0& 1\\1& 0\end{bmatrix}$ 有 $\lambda_1=1, x_1=\begin{bmatrix}1\\1\end{bmatrix},$$ \lambda_2=-1, x_2=\begin{bmatrix}-1\\1\end{bmatrix}$。

  看转置矩阵 $A’$ 与本例中的对称矩阵 $A$ 有什么联系。

  易知 $A=A’+3I$，两个矩阵特征向量相同，而其特征值刚好相差 $3$。也就是如果给一个矩阵加上 $3I$，则它的特征值会加 $3$，而特征向量不变。

  这一点是很容易证明的，如果 $Ax=\lambda x$，则 $(A+3I)x=\lambda x+3x=(\lambda+3)x$，所以 $x$ 还是原来的 $x$ ，而 $\lambda$ 变为 $\lambda+3$。

  但假设我们加的不是 $cI$ （$c$ 为常数）而是其他一般的矩阵 $B$，那么就不能像上面这么做了。比如已知 $Ax=\lambda x, Bx=\alpha x$，那么 $(A+B)x=(\lambda+\alpha)x$ 一般是错误的。问题的关键在于：我们无法相信 $A$ 的特征向量 $x$ 也是 $B$ 的特征向量，也即这两个式子中的特征向量 $x$ 并不一定相同，所以上述两个式子的通常情况是：$Ax=\lambda x, By=\alpha y$ ，它们也就无从相加了。而若 $B=cI$，那么我们总能保证 $A$ 的特征向量 $x$ 也会是 $B$ 的特征向量，因为给定任意向量 $x$，显然都有 $cIx=cx$，也即 $B$ 的特征向量实际上包含了 $A$ 的特征向量。

对于刚刚的例子，我们已经发现一次项系数似乎和矩阵的迹存在关系，更普遍地，能注意到矩阵的特征值之和等于矩阵的迹。同时如果我们计算矩阵 $A$ 的行列式，能发现 $\det(A)=8=\lambda_1\cdot\lambda_2$。下面我们给出两条有关矩阵特征值的性质：

• 矩阵的特征值之和等于矩阵的迹
• 矩阵的特征值之积等于矩阵的行列式

鉴于这两条性质的证明需要用到根与系数的关系，也即韦达定理，所以我们先给予韦达定理的证明。

$$\displaylines{ 给定方程\ a_nx^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\cdots+a_1x+a_0=0\ \ \ (1)\\ 假设上述方程的有根\ x_1,x_2,\cdots,x_n，那么给定方程可改写为如下形式：\\ \qquad\qquad a_n(x-x_1)(x-x_2)(x-x_3)\cdots(x-x_n)=0\ \ \ \ \qquad(2)\\ 根据初高中多项式展开的知识可知：\\对于所有括号只取第一项\ x，则有\ C^n_nx^n=x^n\\所以\ x_n\ 的系数为\ C^n_na_n=a_n，与\ (1)\ 中相符。\\同理，所有括号中我们对其中\ n-1\ 个取第一项，那么\ x^{n-1}\ 的系数为 \\-a_n(x_1+x_2+...+x_n)，也即\ (1)\ 中 \ a_{n-1}=-a_n(x_1+x_2+...+x_n)。\\ \therefore -\frac{x^{n-1}的系数}{x^n的系数}=-\frac{a_{n-1}}{a_{n}}=-\frac{-a_n(x_1+x_2+...+x_n)}{a_n}=(x_1+...+x_n) \\对应到一元二次方程\ ax^2+bx+c=0\ 里即\ x_1+x_2=-\frac{b}{a}。\\ 同理，所有括号中我们都取第二项，那么我们将得到常数项\ (-1)^na_nx_1x_2...x_n\\ 也即\ (1)\ 中\ a_0=(-1)^na_nx_1x_2...x_n。\\ \therefore \frac{常数项}{x^n的系数}=\frac{a_0}{a_n}=\frac{(-1)^na_nx_1x_2...x_n}{a_n}=(-1)^nx_1x_2...x_n\\ \therefore (-1)^n\frac{常数项}{x^n的系数}=x_1x_2...x_n\\ 对应到一元二次方程\ ax^2+bx+c=0\ 里也即\ x_1x_2=(-1)^2\frac{c}{a}=\frac{c}{a} }$$

• 矩阵的特征值之和等于矩阵的迹：$\sum_{i=1}^n \lambda_i=\sum_{i=1}^n a_{ii}$

$$\displaylines{ 证明：设\ A=\begin{bmatrix}a_{11}&a_{12}&a_{13}&\cdots&a_{1n}\\ a_{21}&a_{22}&a_{23}&\cdots&a_{2n}\\a_{31}&a_{32}&a_{33}&\cdots&a_{3n}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&a_{n3}&\cdots&a_{nn}\end{bmatrix}，则\\ \det(A-\lambda I)=\begin{vmatrix}a_{11}-\lambda &a_{12}&a_{13}&\cdots&a_{1n}\\ a_{21}&a_{22}-\lambda&a_{23}&\cdots&a_{2n}\\a_{31}&a_{32}&a_{33}-\lambda&\cdots&a_{3n}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&a_{n3}&\cdots&a_{nn}-\lambda\end{vmatrix}\\ 按行列式的定义可以将其展开成\ n!\ 项非零行列式相加的形式\\除了\ (a_{11}-\lambda)(a_{22}-\lambda)\cdots(a_{nn}-\lambda)\ 项含有所有\ (a_{11}-\lambda),(a_{22}-\lambda),\cdots,(a_{nn}-\lambda)\\ 的\ n\ 个因子外，其他项最多仅含\ (a_{11}-\lambda)(a_{22}-\lambda)...(a_{nn}-\lambda)\ 这些因子中的\ n-2\ 个\\比如\ a_{12}a_{21}(a_{33}-\lambda)...(a_{nn}-\lambda)。\\ \therefore \lambda^n\ 和\ \lambda^{n-1} 只可能来自包含所有因子的\ (a_{11}-\lambda)(a_{22}-\lambda)...(a_{nn}-\lambda)\ 项\\ \therefore \det(A-\lambda I)=(a_{11}-\lambda)(a_{22}-\lambda)\cdots(a_{nn}-\lambda)+\cdots\\=(-1)^n\lambda^{n}+(-1)^{n-1}(a_{11}+a_{22}+\cdots+a_{nn})\lambda^{n-1}+\cdots\\ 于是\ 可知\det(A-\lambda I)\ 的\ \lambda^{n-1}\ 的系数为(-1)^{n-1}(a_{11}+a_{22}+...+a_{nn}) \\令\ \det(A-\lambda I)=0\ 可得特征方程，根据根与系数关系可知：\\特征值之和=特征方程的根之和=-\frac{\lambda^{n-1}项的系数}{\lambda^{n}项的系数}\\ 综上，\lambda_1+\lambda_2+...+\lambda_n(特征值之和)=(a_{11}+a_{22}+...+a_{nn}) }$$

• 矩阵的特征值之积等于矩阵的行列式：$\prod_{i=1}^n\lambda_i=\det(A)$

$$\displaylines{ 证明：设\ A=\begin{bmatrix}a_{11}&a_{12}&a_{13}&\cdots&a_{1n}\\ a_{21}&a_{22}&a_{23}&\cdots&a_{2n}\\a_{31}&a_{32}&a_{33}&\cdots&a_{3n}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&a_{n3}&\cdots&a_{nn}\end{bmatrix}，则\\ \det(A-\lambda I)=\begin{vmatrix}a_{11}-\lambda &a_{12}&a_{13}&\cdots&a_{1n}\\ a_{21}&a_{22}-\lambda&a_{23}&\cdots&a_{2n}\\a_{31}&a_{32}&a_{33}-\lambda&\cdots&a_{3n}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&a_{n3}&\cdots&a_{nn}-\lambda\end{vmatrix}\\ 按行列式的定义可以将其展开成\ n!\ 项非零行列式相加的形式\\这\ n!\ 项中必然存在不包含 任何诸如\ (a_{11}-\lambda),(a_{22}-\lambda),\cdots,(a_{nn}-\lambda)的因子的非零行列式\\ 这样的行列式自然也就不包括\ \lambda\ 项。\\ \det(A-\lambda I)=\underbrace{(a_{11}-\lambda)(a_{22}-\lambda)\cdots(a_{nn}-\lambda)}_{(-1)^n\lambda^{n}+(-1)^{n-1}(a_{11}+a_{22}+...+a_{nn})\lambda^{n-1}}+\underbrace{(\cdots)}_{其他项,包含\ \lambda^{n-2}\ 到\ \lambda\ 的项}+\underbrace{(C)}_{常数项,不包含任何\ \lambda\ 项}\\ 于是可知\ \lambda^n\ 的系数为\ (-1)^n， 令\ \lambda=0，则有\ \det(A)=C。\\ 令\ \det(A-\lambda I)=0\ 可得特征方程，根据根与系数的关系可知：\\ 特征值之积=特征方程的根之积=(-1)^n\frac{常数项}{\lambda^n项的系数}\\ 也即\ \lambda_1\lambda_2...\lambda_3(特征值之积)=\det(A) }$$

• 我们再来看旋转矩阵的例子，旋转 $90^{\circ}$ 的矩阵 $Q=\begin{bmatrix}\cos {90^{\circ}}& -\sin {90^{\circ}}\\\sin {90^{\circ}}& \cos {90^{\circ}}\end{bmatrix}=\begin{bmatrix}0& -1\\1& 0\end{bmatrix} $（作用到向量上能将向量旋转 $90^{\circ}$，用 $Q$ 表示旋转矩阵是因为旋转矩阵是正交矩阵中相当重要的例子）。

  根据上面提到特征值的两个性质：特征值之和等于矩阵的迹，特征值之积等于矩阵的行列式，则对于 $Q$ 矩阵，有 $\begin{cases}\lambda_1+\lambda_2& =0\\\lambda_1\cdot\lambda_2& =1\end{cases}$，再来思考特征值与特征向量的由来，哪些非向量旋转 $90^{\circ}$ 后与自己平行，于是就遇到了麻烦，我们发现，似乎不存在非零向量旋转 $90^{\circ}$ 能与旋转前的自己同向，同时似乎也不存在特征值来满足前面的方程组（$\lambda_1$ 与 $\lambda_2$ 异号但其相乘结果却为正数）。

  由 $\det(Q-\lambda I)=\begin{vmatrix}\lambda& -1\\1& \lambda\end{vmatrix}=\lambda^2+1=0$ 可得特征值为 $\lambda_1=i, \lambda_2=-i$。这两个特征值显然满足 $\begin{cases}\lambda_1+\lambda_2& =0\\\lambda_1\cdot\lambda_2& =1\end{cases}$，但这两个特征值并不是实数。我们发现，即使矩阵全是实数，其特征值也可能不是实数，本例中的实数矩阵其特征值就为一对共轭复数。

  实际上，如果矩阵是对称的或者说接近对称的，那么特征值一般就是实数。如果越不对称，就像上面旋转矩阵的例子，$Q^T=-Q$，这说明旋转矩阵是一个反对称的矩阵，这样的矩阵，其特征值往往就是纯虚数。

  实数特征值让特征向量伸缩而虚数让其旋转。

  到现在为止我们看到，对于好的矩阵（最上面提到的置换矩阵）有实特征值及正交的特征向量，对于不好的矩阵（$90^{\circ}$ 旋转矩阵）有纯虚的特征值。

  上面我们提到了旋转矩阵，下面将就二维情况进行推导

  

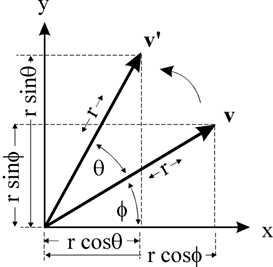
  如图所示点 $v$ 绕原点旋转 $\theta$ 角，得到点 $v’$，假设 $v$ 点的坐标是 $(x,y)$，那么可以推导得到 $v’$ 的坐标 $(x’,y’)$

  $$\displaylines{ 首先假设原点到\ v\ 的距离是\ r，v\ 点对应的向量与\ x\ 轴的夹角是\ \phi，那么：\\ x=r\cos\phi\quad y=r\sin\phi\\ x'=r\cos(\theta+\phi)\quad y'=r\sin(\theta+\phi)\\ 通过三角函数展开易得：\\ x'=r\cos\theta\cos\phi-r\sin\theta\sin\phi\\ y'=r\sin\theta\cos\phi+r\cos\theta\sin\phi\\ 用\ x\ 和\ y\ 进行替换有：\\ x'=x\cos\theta-y\sin\theta\\ y'=x\sin\theta+y\cos\theta }$$

• 再来看一个更糟的情况，$A=\begin{bmatrix}3& 1\\0& 3\end{bmatrix}$。

  这是一个三角矩阵，对于这样的矩阵我们可以直接得出其特征值，即矩阵对角线上的元素。$\det(A-\lambda I)=\begin{vmatrix}3-\lambda& 1\\0& 3-\lambda\end{vmatrix}=(3-\lambda)^2=0$，于是 $\lambda _1=3,\lambda_2=3$。特征值为实数，看上去似乎很好，但实际上这是非常糟糕的情况，这体现在特征向量上。

  代入特征值计算特征向量：代入 $\lambda_1=3$ 得 $(A-\lambda I)x=\begin{bmatrix}0& 1\\0& 0\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix}$，算出 $x_1=\begin{bmatrix}1\\0\end{bmatrix}$。而当我们把第二个特征值 $\lambda_2=3$ 代入时，等式和之前是一样的，又得到相同的向量。于是，我们根本无法找到另外一个与 $x_1$ 线性无关的特征向量了。

  本例中的矩阵是一个退化矩阵，我们只能找到一个方向上的特征向量而不是两个。对于一个退化矩阵，重复的特征值在特殊情况下可能导致特征向量的短缺。