Lec20 - 克拉默法则、逆矩阵、体积

第 20 课 克拉默法则、逆矩阵、体积

本节是关于行列式的最后一课，经过前两节课的努力，我们研究了行列式的性质，并从性质出发得到了行列式的求解方法。这一节我们将介绍行列式的应用，主要包含三个方面：求逆矩阵，克莱姆法则和体积。

求逆矩阵 $A^{-1}$

早在第三课，我们就已经介绍了求解逆矩阵的方法：高斯-若尔当求逆法。高斯-若尔当求逆法对于数值计算无懈可击，但很难想象这是如何做到的，也许我们需要一个更直观的逆矩阵的代数表达式，这就用到了行列式的知识。

我们先给出二阶逆矩阵公式：$\begin{bmatrix}a& b\\c& d\end{bmatrix}^{-1}=\frac{1}{ad-bc}\begin{bmatrix}d& -b\\ -c& a\end{bmatrix}$ ，从 $2\times 2$ 的情况中，我们能够看出一些端倪。

首先关注公式的分母，其为行列式的值，也许一般逆矩阵公式其中一部分正是 $1$ 除以矩阵的行列式，这一部分是合理的，因为只有当行列式的值不等于 $0$ 时，矩阵才是可逆的。

接下来的问题是，公式右边那一块矩阵是什么？从代数余子式的角度来考虑，左上角的 $d$ 是原矩阵中 $a$ 的代数余子式，右上角的 $-b$ 是原矩阵中 $c$ 的代数余子式。实际上，公式右边这一块矩阵就是由代数余子式组成的，为代数余子式矩阵 $C$ 的转置，我们一般称其为伴随矩阵，记为 $C^T$。

假设一般地，矩阵 $A$ 的逆矩阵公式为：

$$\displaylines{ A^{-1}=\frac{1}{\det (A)}C^T }$$

$A^{-1}$ 是一个 $n\times n$ 的矩阵，$\det(A)$ 是 $n$ 个元素乘积的组合（行列式公式），$C^T$ 中各元素是 $n-1$ 个元素乘积的组合。

我们针对于特定的 $2\times 2$ 情况找出一个等式，并从中归纳得到上式，但实际上，以上逆矩阵公式是否真的成立呢？对于 $2\times 2$ 很好但对于 $n\times n$ 的情况是否成立呢？显然，我们需要进一步证明这个公式：

$$\displaylines{ 已知 A有逆矩阵，也即 AA^{-1}=I，要证 A^{-1}=\frac{1}{\det (A)}C^T\\ 对逆矩阵公式两端同乘以 A，易得 I=AA^{-1}=\frac{1}{\det (A)}AC^T\\ 化简有 AC^T=(\det A)I，若该式成立那么原式成立\\ 将化简结果写成矩阵形式有：\\ \begin{bmatrix}a_{11}& a_{12}& \cdots& a_{1n}\\\vdots& \vdots& \ddots& \vdots\\a_{n1}& a_{n2}& \cdots& a_{nn}\end{bmatrix}\begin{bmatrix}C_{11}& \cdots& C_{n1}\\C_{12}& \cdots& C_{n2}\\\vdots& \ddots& \vdots\\C_{1n}& \cdots& C_{nn}\end{bmatrix}=\overbrace{\begin{bmatrix}det(A)&0&\cdots&0\\0&det(A)&\cdots&0\\\vdots&\vdots &\ddots&\vdots\\0&0&\cdots&det(A)\end{bmatrix}}^{D} }$$

• 我们先来证明对角元素均为 $\det(A)$：

  对于这两个矩阵的乘积，观察其结果的元素 $D_{11}=a_{11}C_{11}+a_{12}C_{12}+\cdots+a_{1n}C_{1n}$，显然这正是上一讲提到的将行列式按第一行展开的结果（我们需要对这种一个因子乘以一个代数余子式的形式足够敏感），所以 $D_{11}=\det(A)$。同理，对 $D_{22}, \cdots, D_{nn}$ 都有 $D_{ii}=\det(A)$，对角元素均为 $\det(A)$ 得证。

• 然后我们再来证明非对角元素均为 $0$：我们把目光放到 $D_{12}$ 上，易得$D_{12}=a_{11}C_{21}+a_{12}C_{22}+\cdots+a_{1n}C_{2n}$，虽然知道公式，但我们仍无法求出 $D_{12}$。

  教授给了一种非常巧妙的思路：我们知道 $D_{22}=a_{21}C_{21}+a_{22}C_{22}+\cdots+a_{2n}C_{2n}=\det(A)$，那什么时候 $D_{22}$ 会与 $D_{12}$ 相等呢？显然，当 $a_{11}=a_{21},a_{12}=a_{22},…,a_{1n}=a_{2n}$ 的时候，也即 $A$ 中第一行和第二行相等的时候有， $D_{22}=D_{12}$。所以我们构造一个这样的矩阵 $A_s$ 有：

  $$\displaylines{ A_{s}=\begin{bmatrix}a_{11}& a_{12}& \cdots& a_{1n}\\a_{11}& a_{12}& \cdots& a_{1n}\\a_{31}& a_{32}& \cdots& a_{3n}\\\vdots& \vdots& \ddots& \vdots\\a_{n1}& a_{n2}& \cdots& a_{nn}\end{bmatrix} }$$

  注意到 $A_s$ 第一行和第二行相同，所以 $\det(A_s)=0$ ，所以 $D_{12}=0$。

  推广到 $n$ 阶，元素 $D_{1i}=a_{11}C_{i1}+a_{12}C_{i2}+\cdots+a_{1n}C_{in}$，按照同样的办法，我们可以构造一个矩阵 $A_s$，该矩阵的第 $i$ 行与第一行相同，所以 $D_{1i}=0$ 。使用这种思路，我们容易证得所有非对角元素都为 $0$。

综上，$AC^T=\det(A)I$ 得证，故 $A^{-1}=\frac{1}{\det (A)}C^T$ 得证。

有了逆矩阵公式，我们能够清楚地看到，当改变原矩阵中的一个元素时，会给逆矩阵带来什么样的变化：$\det(A)$ 发生了变化，$C^T$ 也发生了变化，总之这帮助我们理解原矩阵的变化对逆矩阵的影响。

---

克莱姆法则

我们现在有了逆矩阵的计算公式，所以对 $Ax=b$ 现在有：

$$\displaylines{ x=A^{-1}b=\frac{1}{\det (A)}C^Tb }$$

更进一步地，我们考虑 $x$ 的分量 $x_i$：

$$\displaylines{ x_i=\frac{Row_i\ of\ C^T}{\det(A)}b=\frac{\det (B_i)}{\det (A)} }$$

其中矩阵 $B_i$ 是向量 $b$ 替代矩阵 $A$ 的第 $i$ 列所得到的新矩阵，这也即克莱姆法则。

从 $(Row_i\ of\ C^T)\ b$ 到 $\det (B_i)$ 的具体过程解析如下：

先来观察 $x=\frac{1}{\det (A)}C^Tb$，我们将得到的解 $x$ 拆分开来，对 $x$ 的第一个分量有 $x_1=\frac{y_1}{\det (A)}$，这里 $y_1$ 是一个数值，其值为 $y_1=b_1C_{11}+b_2C_{21}+\cdots+b_nC_{n1}$。当我们看到数字与代数余子式乘之积求和时，都应该联想到求行列式，也就是说 $y_1$ 可以看做是一个矩阵沿其中的 $b$ 列而展开所得的行列式，我们设这个矩阵为 $B_1$，故有 $x_1=\frac{\det (B_1)}{\det (A)}$。同理有 $x_2=\frac{\det (B_2)}{\det (A)}$，$x_3=\frac{\det (B_3)}{\det (A)}$等等。

由 $y_1$ 的形式可知，$b$ 不仅仅是 $B_1$ 中的列，而且还是第一列，因此：

$$\displaylines{ B_1=\begin{bmatrix}b_1& a_{12}& \cdots& a_{1n}\\b_2& a_{22}& \cdots& a_{2n}\\\vdots& \vdots& \ddots& \vdots\\b_n& a_{n2}& \cdots& a_{nn}\end{bmatrix} }$$

也即，将矩阵 $A$ 的第一列变为 $b$ 向量而得到的新矩阵。

我们也容易验证 $\det(B_1)=y_1$：沿第一列展开得到 $b_1C_{11}+b_2C_{21}+\cdots+b_nC_{n1}$。

一般地，对于 $B_i$ 有 $\begin{bmatrix}{a_1}&{a_2}&\cdots&{a_{i-1}}&{b}&{a_{i+1}}&\cdots&{a_n}\end{bmatrix}$，即将矩阵 $A$ 的第 $i$ 列变为 $b$ 向量而得到的新矩阵，所以对于解的分量有 $x_i=\frac{\det B_i}{\det A}$。

克拉默法则很漂亮，但它并不实用。若使用克拉默法则求解 $Ax=b$，那么我们需要求出 $n+1$ 个矩阵的行列式（$n$ 个 $B_i$ 矩阵，$1$ 个 $A$ 矩阵），相比我们之前介绍的消元的方法，克拉默法则的计算量太大了。虽然克拉默法则不实用，但它提供了一个代数表达式，让你能代数运算而不只是写算法。

---

行列式的几何意义 —— 体积

$3$ 阶矩阵 $A$ 的行列式的绝对值 $\vert{\det(A)}\vert$ 等于以矩阵 $A$ 行（列）向量为边所构成的平行六面体的体积。行列式的符号正负对应左手系和右手系。

先给出命题：对于 $3\times 3$ 矩阵，其行列式的绝对值等于一个箱子的体积。

来看三维空间中的情形，对于 $3$ 阶方阵 $A$，取第一行 $(a_{11},a_{12},a_{13})$。令其为三维空间中点 $A_1$ 的坐标，同理有点 $A_2,A_3$。连接这三个点与原点可以得到三条边，使用这三条边展开得到一个平行六面体，而 $\vert{\det(A)}\vert$ 就是该平行六面体的体积。

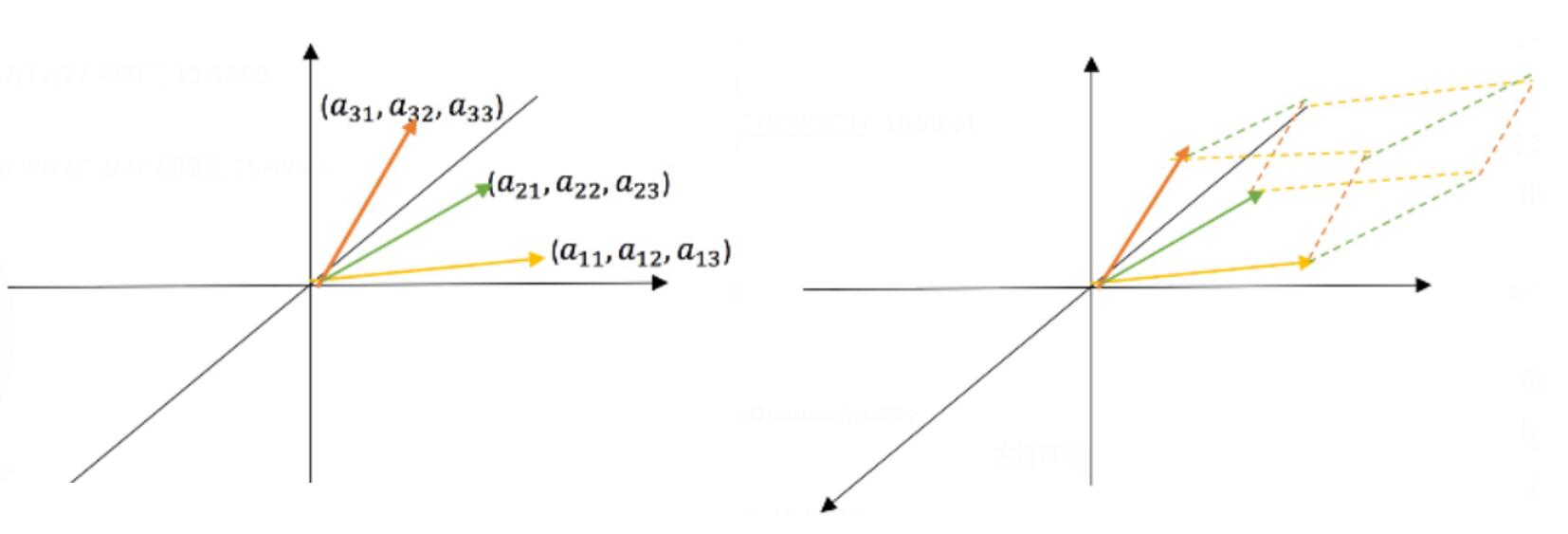
对于三阶单位矩阵 $I$，其体积为 $\det(I)=1$ ，此时这个箱子是一个单位立方体。这其实也印证了前面学过的行列式性质 $1$。

基于这一点，于是我们想：如果能够继续证明箱子体积具有行列式的三大基础性质，而三大基础性质定义了行列式，那么箱子体积就一定等于行列式。这是一个非常巧妙的间接证明的方法。

接下来我们接着看体积是否具有行列式的性质 $2$ 和 $3$。

首先对于行列式性质 $2$，我们交换两行并不会改变箱子的大小，同时行列式的绝对值也没有改变，性质 $2$ 得证。

在验证性质 $3$ 之前，我们先再取正交矩阵 $Q$ 为例来研究其体积与其行列式的关系。

显然 $3$ 阶正交矩阵实际上所形成的箱子也是一个单位立方体，只不过略有旋转。既然如此，那么箱子的体积显然是 $1$。那么 $3$ 阶正交矩阵是否其行列式的绝对值也为 $1$ 呢？

$$\displaylines{ 已知对于正交矩阵（标准正交矩阵），有\ Q^TQ=I\\ 等式两边取行列式易得\quad \det(Q^TQ)=1=\det(Q^T)\det(Q)\\ 又根据行列式性质\ 10\ 有\quad \det(Q^T)=\det(Q)\\ \therefore (\det(Q))^2=1,\vert \det(Q)\vert =1 }$$

与体积相等，符合命题。

接下来在考虑不再是“单位”的立方体，即长方体。 假设 $Q$ 矩阵的第一行翻倍得到新矩阵 $Q’$，此时箱子变为在第一行方向上增加一倍的长方体箱子，也就是两个“标准正交箱子”在第一行方向上的堆叠。易知这个长方体箱子是原来体积的两倍，而根据行列式性质 $3.a$ 有 $2\det(Q)=\det(Q’)$ ，这说明箱子体积也符合行列式的数乘性质。

现在我们只剩下性质 $3.b$ 没有进行验证了。为方便，我们将在 $2$ 阶矩阵上进行验证。

首先指出，对于 $2$ 阶矩阵，其行列式等于一个平行四边形的面积。我们来看 $2$ 阶方阵的情形。在二阶情况中，行列式就是一个求平行四边形面积的公式，原来我们求由四个点 $(0,0), (a,b), (c,d), (a+c,b+d)$ 围成的四边形的面积，需要先求四边形的底边长度，再作高得到高度来求解；而现在从线性代数的角度出发，令 $A=\begin{bmatrix}a&b\\c&d\end{bmatrix}$，只需要计算 $\det (A)=ad-bc$ 即可（更加常用的是求由 $(0,0),(a,b),(c,d)$ 围成的三角形的面积，即 $\frac{1}{2}(ad-bc)$）。

那么 $2$ 阶方阵的面积是否具有行列式的性质 $3.b \begin{vmatrix}a+a’& b+b’\\c& d\end{vmatrix}=\begin{vmatrix}a& b\\c& d\end{vmatrix}+\begin{vmatrix}a’& b’\\c& d\end{vmatrix}$ 呢？我们很容易从几何上看出这一点，如下图：

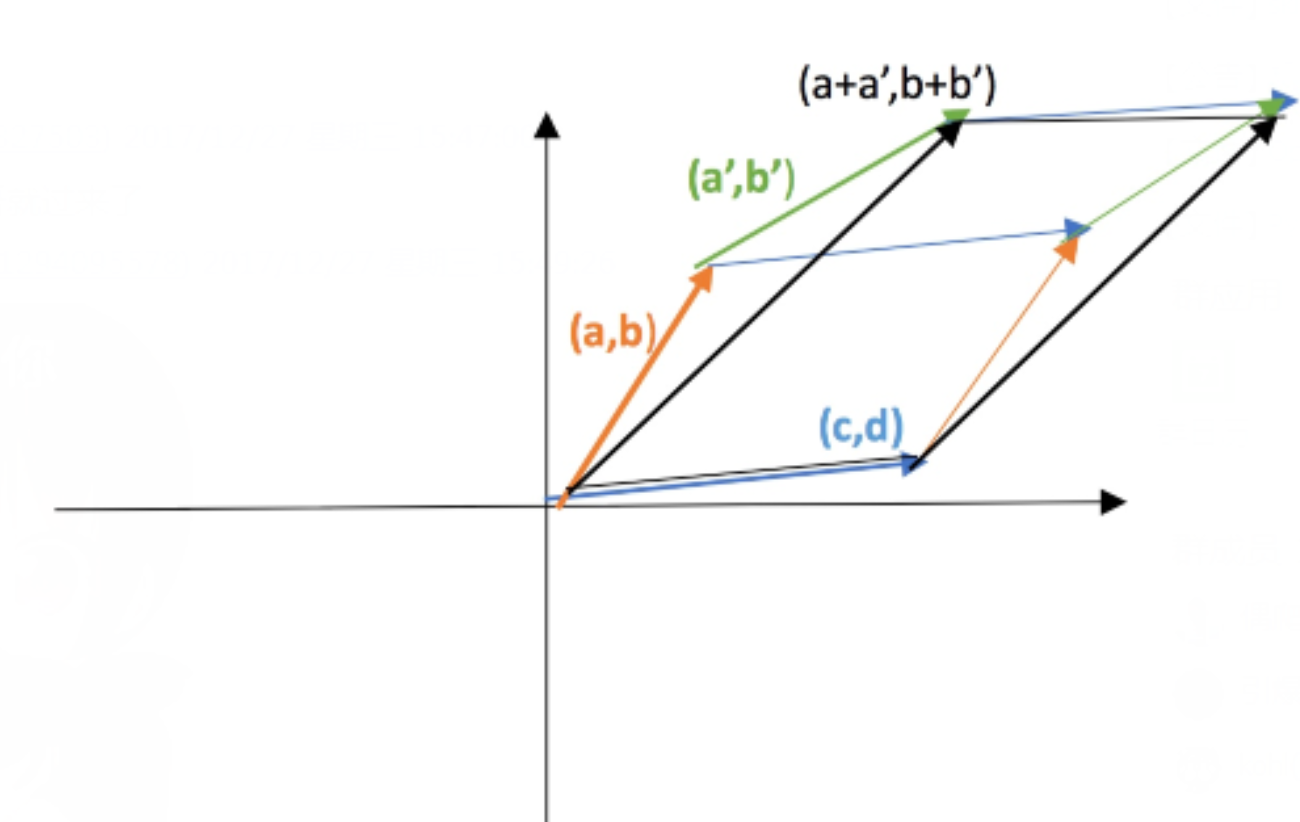
上图中，左右两边的三角形显然是全等三角形，故得证。

此外，采用底乘高方式求解平行四边形面积一样蕴含了性质 $3.b$：

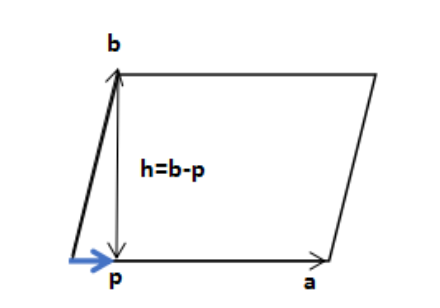
如上图所示，${a}$ 和 ${b}$ 围成的平行四边形的面积，等于 ${a}$ 和 ${h}$ 的长度之积，若写成行列式形式有 $\begin{vmatrix}a_1&a_2\\h_1& h_2\end{vmatrix}$。由上面的内容可知该平行四边形的面积还可以是 $\begin{vmatrix}a_1&a_2\\b_1& b_2\end{vmatrix}$，$\begin{vmatrix}a_1&a_2\\b_1& b_2\end{vmatrix}=\begin{vmatrix}a_1&a_2\\h_1& h_2\end{vmatrix}$ 的证明就用到了性质 $3.b$：

$$\displaylines{ \begin{vmatrix}a_1&a_2\\h_1& h_2\end{vmatrix}=\begin{vmatrix}a_1&a_2\\b_1-p_1& b_2-p_2\end{vmatrix}\stackrel{性质3.b}{=}\begin{vmatrix}a_1&a_2\\b_1& b_2\end{vmatrix}-\begin{vmatrix}a_1&a_2\\p_1& p_2\end{vmatrix}\\ 由图可知 {p} 与 {a} 共线，彼此线性相关，故 \begin{vmatrix}a_1&a_2\\p_1& p_2\end{vmatrix}=0\\ 因此 \begin{vmatrix}a_1&a_2\\b_1& b_2\end{vmatrix}=\begin{vmatrix}a_1&a_2\\h_1& h_2\end{vmatrix},得证 }$$

可以看到，底乘高方式计算平行四边形面积在行列式等于面积（体积）的命题中仍然是自洽的。

最后，我们再将行列式求解三角形面积的方法一般化。在一般情形下，由点 $(x_1,y_1), (x_2,y_2), (x_3,y_3)$ 围成的三角形面积等于 $\frac{1}{2}\begin{vmatrix}x_1& y_1& 1\\x_2& y_2& 1\\x_3& y_3& 1\end{vmatrix}$ （第三列全为 $1$ 反映了三点共面），计算时分别用第二行减去第一行，第三行减去第一行（这些操作实际作用是将三角形移动到原点 ），得到 $\frac{1}{2}\begin{vmatrix}x_1& y_1& 1\\x_2-x_1& y_2-y_1& 0\\x_3-x_1& y_3-y_1& 0\end{vmatrix}$，再按照第三列将行列式展开，得到三角形面积等于 $\frac{1}{2}((x_2-x_1)(y_3-y_1)-(x_3-x_1)(y_2-y_1))$。