Lec17 - 正交矩阵和 Gram-Schmidt 正交化

第 17 课 正交矩阵和 Gram-Schmidt 正交化

上一课最后我们简单介绍了标准正交向量组的概念，这一课中，我们将深入介绍标准正交向量组的性质和优点，以及将一组向量化为标准正交向量组的方法：Gram-Schmidt 正交化。

标准正交向量与正交矩阵

上一节我们介绍过标准正交向量，我们通过一个式子进行回顾。设 $q$ 是标准正交向量组中的任意向量，则

$$\displaylines{ q_{i}^{T} q_{j}\left\{\begin{array}{l}{0 \ldots . .(i \neq j)} \\ {1 \ldots . .(i=j)}\end{array}\right. }$$

这很好地表现了标准正交向量组内各向量的性质：不同向量之间相互垂直（正交），向量长度都为 1（标准）。

标准正交向量组又被称为标准正交基，显然，相互垂直的各列一定是线性无关的。

为什么我们这么执着于标准正交向量呢？在后续我们就能看到标准正交向量能够极大的简化计算，许多数值线性代数都建立在标准正交向量的基础上，因为它们容易操控，它们从不上溢或下溢。

我们再介绍另外一个概念，标准正交矩阵。所谓标准正交矩阵 $Q$，就是将标准正交向量组中的向量 $q_{1}, q_{2},\cdots,q_{n}$ 列到一个矩阵中去：

$$\displaylines{ Q=\left[\begin{array}{llll}{q_{1}} & {q_{2}} & {\cdots} & {q_{n}}\end{array}\right] }$$

这样的标准正交矩阵有一个很好的性质：

$$\displaylines{ Q^TQ=\begin{bmatrix}q_1^T\\q_2^T\\\vdots\\q_n^T\end{bmatrix}\begin{bmatrix}q_1&q_2&\cdots&q_n\end{bmatrix}=\begin{bmatrix}1& 0& \cdots& 0\\0& 1& \cdots& 0\\\vdots& \vdots& \ddots& \vdots\\0& 0& \cdots& 1\end{bmatrix}=I }$$

注意，是 $Q^TQ=I$ 而非 $QQ^T=I$。

特别地，当 $Q$ 是方阵时，我们将这样的矩阵 $Q$ 称为正交矩阵。

为什么我们要单独将 $Q$ 是方阵的情况拎出来呢？这是因为当标准正交矩阵 $Q$ 为方阵时，其必有逆矩阵，很明显，由上面的 $Q^TQ=I$ 可知，$Q$ 若为正交矩阵，其逆矩阵正是 $Q^T$，也即 $Q^T=Q^{-1}$。可以举一些例子：

• 回想我们在很久之前提到过的置换矩阵，当时也说明了置换矩阵 $P$ 具有性质：$P^T=P^{-1}$，而显然置换矩阵正是一个正交矩阵：$P=\begin{bmatrix}0& 1& 0\\1& 0& 0\\0& 0& 1\end{bmatrix}$，则 $Q^T=\begin{bmatrix}0& 1& 0\\0& 0& 1\\1& 0& 0\end{bmatrix}$，易得 $Q^TQ=I$。
• 另一个例子是我们上一讲介绍过的标准正交向量组：$\left[\begin{array}{c}{\cos \theta} \\ {\sin \theta}\end{array}\right],\left[\begin{array}{c}{-\sin \theta} \\ {\cos \theta}\end{array}\right]$ 。写成矩阵形式即为 $Q=\left[\begin{array}{cc}{\cos \theta} & {-\sin \theta} \\ {\sin \theta} & {\cos \theta}\end{array}\right]$ ，显然该矩阵也有 $Q^TQ=I$。
• $\left[\begin{array}{cc}{1} & {1} \\ {1} & {-1}\end{array}\right]$ 是正交矩阵吗？不是，因为虽然这个矩阵内各列正交，但列向量长度不为 $1$，我们还需要再对其进行单位化（标准化），单位化以后得到 $Q=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}{1} & {1} \\ {1} & {-1}\end{array}\right]$ ，这个矩阵是正交矩阵。
• 使用上一个例子中的矩阵 $Q=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}{1} & {1} \\ {1} & {-1}\end{array}\right]$，令 $Q’=c\begin{bmatrix}Q& Q\\Q& -Q\end{bmatrix}$ ，取合适的 $c$ 以使得向量长度为 $1$ 也可以构造出一个正交矩阵：$Q=\frac{1}{2}\begin{bmatrix}1& 1& 1& 1\\1& -1& 1& -1\\1& 1& -1& -1\\1& -1& -1& 1\end{bmatrix}$，这种构造方法以阿德玛（Adhemar）命名，我们现在知道的是这种构造方法在 $Q$ 为 $2, 4, 16, 64, \cdots$ 维矩阵时是有效的，但是没有人知道，究竟哪些维数的正交矩阵可以由 $1$ 和 $-1$ 们构成，阿德玛矩阵是一种只有 $1$ 和 $-1$ 的正交矩阵，有些维度可以，但有些维度就不行，比如说 $5$ 维的矩阵就不可能是阿德玛矩阵，这个比较简单，但有些大小没人能确切地说，能不能由 $1$ 和 $-1$ 构成。

上面我们介绍了标准正交矩阵 $Q$ 的各种性质，这是一种新的性质优良的矩阵，这样的矩阵能够极大地简化计算，比如：投影矩阵！

上一讲中，我们提到，投影矩阵 $P=A(A^TA)^{-1}A^T$，那么到 $A$ 是标准正交矩阵 $Q$ 的时候，根据标准正交矩阵的性质易得：$Q(Q^TQ)^{-1}Q^T=QIQ^T=QQ^T$。特别地，当 $Q$ 还是方阵的时候，由于此时 $Q^T=Q^{-1}$，所以投影矩阵能够进一步化简为 $I$。

$$\displaylines{ P=A(A^TA)^{-1}A^T\xrightarrow{A是标准正交矩阵Q}P=QQ^T\xrightarrow{A还是方阵（也即A是正交矩阵）}P=I }$$

化为 $P=QQ^T$ 之后，我们很容易验证投影矩阵的两条性质：

• 投影矩阵为对称矩阵：$(QQ^T)^T=(Q^T)^TQ^T=QQ^T$。
• 投影两次等于投影一次：$(QQ^T)(QQ^T)=Q(Q^TQ)Q^T=QQ^T$。

可以看到 $P$ 的形式得到的极大的化简，实际上很多复杂的方程，在使用标准正交基之后都会变得非常简单。

考虑我们最近讲过的最重要的方程，正规方程 $A^TA\hat{x}=A^Tb$，现在变为了 $Q^TQ\hat{x} = Q^Tb$，也就是 $\hat{x}=Q^Tb$，分解开来看就是 $\hat x_i=q_i^Tb$，这个式子在很多数学领域都有重要作用。当我们知道标准正交基，则在第 $i$ 个基方向上的投影等于 $q_i^Tb$。

---

Gram-Schmidt 正交化

我们已经看到标准正交向量的性质特别好，但更多时候我们见到的是线性无关向量组，有没有一种方法能够将线性无关向量组转换为标准正交基呢？这也即今天要讲的第二个内容，Gram-Schmidt 正交化。

在介绍它之前，我们需要先说明，格拉姆-施密特正交化的缺点在于，由于要求的单位向量，我们不可避免地要除以向量的长度，而这个过程很容易产生根号，所以最终产生的标准正交向量组经常会带有根号。

Gram-Schmidt 正交化的过程如下：

$$\displaylines{ 线性无关向量a,b\xrightarrow{Graham}正交向量A,B\xrightarrow{Schmidt}标准正交向量q_1=\frac{A}{\|A\|},q_2=\frac{B}{\|B\|} }$$

可以看到 Schmidt 也即单位化的过程是很简单的，正交化的关键在于找到 $A,B$。

我们先从简单的情况开始，假设有两个线性无关的向量 $a,b$：

怎样将其转换为两个相互正交的向量呢？容易联想到我们之前学习的投影，我们可以这样做：

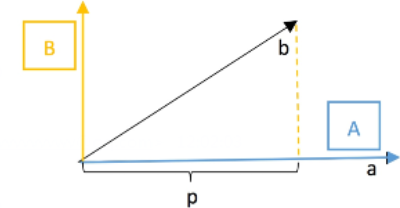
直接将 $a$ 向量定为 $A$ 向量，而后，我们将 $b$ 向量投影到 $a$ 向量上得到 $p$，注意到，此时误差向量 $e=b-p$ 恰好就垂直于 $A$ 向量，故令 $B=b-p$ 有：

$$\displaylines{ B=b-p=b-Pb=b-A(A^TA)^{-1}A^Tb }$$

需要强调的是，上述公式中的 $A,B$ 指的都是向量，故有 $B=b-\frac{AA^Tb}{A^TA}$，其中 $A^TA$ 是一个内积标量值，而 $AA^T$ 是一个矩阵，注意到 $\frac{A\color{red}{A^Tb}}{\color{red} {A^TA}}$ 中标红部分都是内积标量值，故我们更倾向于让分子中的 $A^Tb$ 先相乘，把 $A$ 向量放到后面，也即写成这样的形式 $B=b-\frac{A^Tb}{A^TA}A$。

检查一下是否满足 $A\bot B$：

$$\displaylines{ A^TB=A^Tb-A^T\frac{A^Tb}{A^TA}A=A^Tb-\frac{A^TA}{A^TA}A^Tb=0 }$$

$A,B$ 正交，求得 $A,B$ 之后，剩下的内容就只是简单的单位化了：$q_1=\frac{A}{\left|A\right|}, q_2=\frac{B}{\left|B\right|}$。

同样的道理，如果我们有三个线性无关的向量 $a,b,c$，我们如何进行 Gram-Schmidt 正交化呢？

按照流程，我们首先要得到 $A,B,C$，前两个向量 $A,B$ 我们已经得到了，现在我们要求第三个向量同时垂直于 $A,B$。

我们依然可以按照上面的思想来求解，也即从 $c$ 中减去其在 $A,B$ 上的分量，即可得到与 $A,B$ 正交的 $C$：

$$\displaylines{ C=c-\frac{A^Tc}{A^TA}A-\frac{B^Tc}{B^TB}B }$$

再把它们单位化：$q_1=\frac{A}{\left|A\right|}, q_2=\frac{B}{\left|B\right|}, q_3=\frac{C}{\left|C\right|}$。

下面我们通过一个简单的例子来试验一遍：

假设 $a=\begin{bmatrix}1\\1\\1\end{bmatrix}, b=\begin{bmatrix}1\\0\\2\end{bmatrix}$，求标准正交矩阵 $Q$。

$$\displaylines{ 首先,\quad A=a=\begin{bmatrix}1\\1\\1\end{bmatrix}\\ 根据公式有,\quad B=b-\frac{A^Tb}{A^TA}A=\begin{bmatrix}1\\0\\2\end{bmatrix}-\frac{3}{3}\begin{bmatrix}1\\1\\1\end{bmatrix}=\begin{bmatrix}0\\-1\\1\end{bmatrix}\\ 验证正交性有,\quad A^TB=0\\ 最后再进行单位化,\quad q_1=\frac{1}{\sqrt 3}\begin{bmatrix}1\\1\\1\end{bmatrix},\quad q_2=\frac{1}{\sqrt 2}\begin{bmatrix}1\\0\\2\end{bmatrix}\\ 则标准正交矩阵为\quad Q=\begin{bmatrix}\frac{1}{\sqrt 3}& 0\\\frac{1}{\sqrt 3}& -\frac{1}{\sqrt 2}\\\frac{1}{\sqrt 3}& \frac{1}{\sqrt 2}\end{bmatrix} }$$

这就是 Gram-Schmidt 正交化方法。对比原始矩阵 $A=\left[\begin{array}{ll}{1} & {1} \\ {1} & {0} \\ {1} & {2}\end{array}\right]$ 和标准正交矩阵 $Q=\left[\begin{array}{cc}{1 / \sqrt{3}} & {0} \\ {1 / \sqrt{3}} & {-1 / \sqrt{2}} \\ {1 / \sqrt{3}} & {1 / \sqrt{2}}\end{array}\right]$，观察两个矩阵的列空间，它们是相同的，也就是说我们的正交化过程从头到尾都是在同一个空间（列空间）中进行的，正交化过程本质不过是矩阵各列的列变换（比如 $B=b-\frac{A^Tb}{A^TA}A$，其中 $b$ 是原始的列向量，$\frac{A^Tb}{A^TA}$ 是标量值，$A$ 是原始的列向量 $a$），最后得到了一个更好的标准正交基。

---

QR 分解

我们曾经用矩阵的眼光审视消元法，故有 $A=LU$，这即是消元法的矩阵表示。

以同样的眼光来看待 Gram-Schmidt 正交化，故有 $A=QR$，这既是 Gram-Schmidt 正交化的矩阵表示。

设 $A$ 有两个列向量：$\Bigg[a_1\ a_2\Bigg]$，标准正交化后有 $\Bigg[a_1\ a_2\Bigg]=\Bigg[q_1\ q_2\Bigg]\begin{bmatrix}a_1^Tq_1& a_2^Tq_1\\a_1^Tq_2& a_2^Tq_2\end{bmatrix}$，而左下角的 $a_1^Tq_2$ 为 $0$。$A=QR$ 的重点在于，$R$ 是一个上三角矩阵，这是因为后来构造的向量总是正交于先前的向量。