Lec16 - 投影矩阵和最小二乘法

第 16 课 投影矩阵和最小二乘法

本章将深入研究投影矩阵，同时对上一课最后引出的最小二乘法做进一步地讲解。最后引出标准正交向量组等概念。

投影矩阵

上一章已经介绍过投影矩阵 $P=A(A^TA)^{-1}A^T$。我们知道，投影矩阵 $P$ 与向量 $b$ 相乘将会把 $b$ 投影到 $A$ 的列空间中。那么现在我们来考虑两个极端的例子，这两个极端的例子将会加深我们对投影矩阵的理解。

• 如果 $b$ 在矩阵 $A$ 的列空间里， 那么 $Pb=b$

  $$\displaylines{ 证明：如果b在矩阵A的列空间里，那么必然有Ax=b\\ Pb=A(A^TA)^{-1}A^Tb=A(A^TA)^{-1}A^TAx=AIx=Ax=b }$$

• 如果 $b$ 垂直于矩阵 $A$ 的列空间，那么 $Pb=0$

$$\displaylines{ 证明：b垂直于A的列空间，根据正交补的概念\\ 可知b是左零空间中的向量\\ \therefore A^Tb=0\\ \therefore Pb=A(A^TA)^{-1}A^Tb=A(A^TA)^{-1}0=0 }$$

通过上面两个极端的例子，我们可以看出来，向量 $b$ 总可以分为两个分量，一个分量在 $A$ 的列空间中，另一个分量垂直于 $A$ 的列空间（也即在 $A$ 的左零空间中）。而上述投影矩阵的作用就是保留列空间中的分量 $p$，去掉左零空间中的分量 $e$。

可以通过一幅图来表示这个关系：

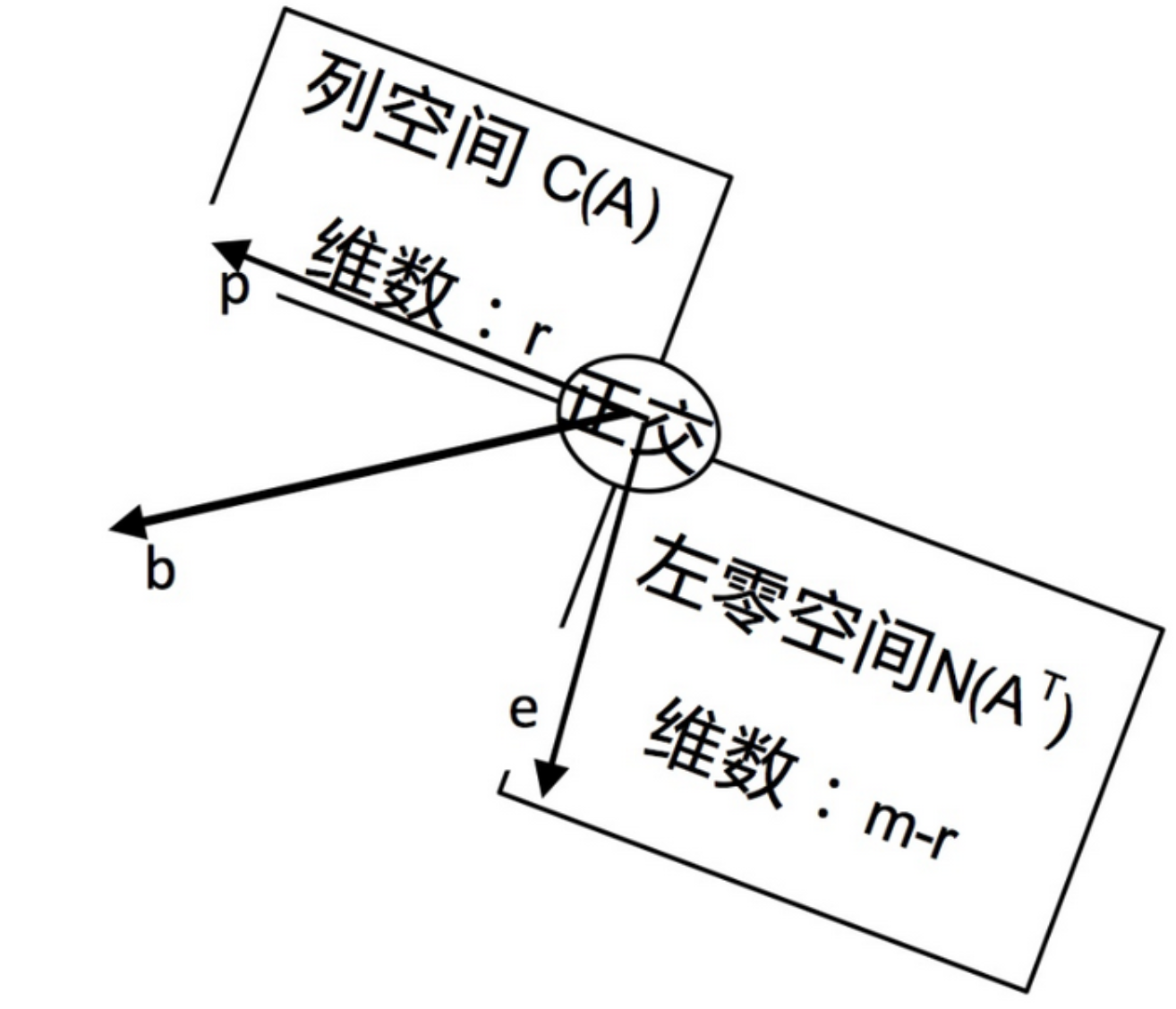
$P$ 把 $b$ 投影到 $A$ 的列空间上得到 $p$。那么，是否存在另外一个投影矩阵把 $b$ 投影到 $A$ 的左零空间上得到 $e$ 呢？由 $b=e+p，p=Pb$ 可得 $e=b-p=b-Pb=(I-P)b$。这里的 $I-P$ 就是 $A$ 的左零空间上的投影矩阵，它具有和 $P$ 一样的性质（对称性与平方不变性）。

---

最小二乘法

回到上一讲最后我们提到的关于最小二乘法的例题：

没有直线能经过图中的三个点，所以我们需要找到一条最优的直线 $y=C+Dx$ 来拟合图中的三个点，这里的最优指的是该直线距离图中三个点 $(1,1)\ (2,2)\ (3,2)$ 的总误差最小！

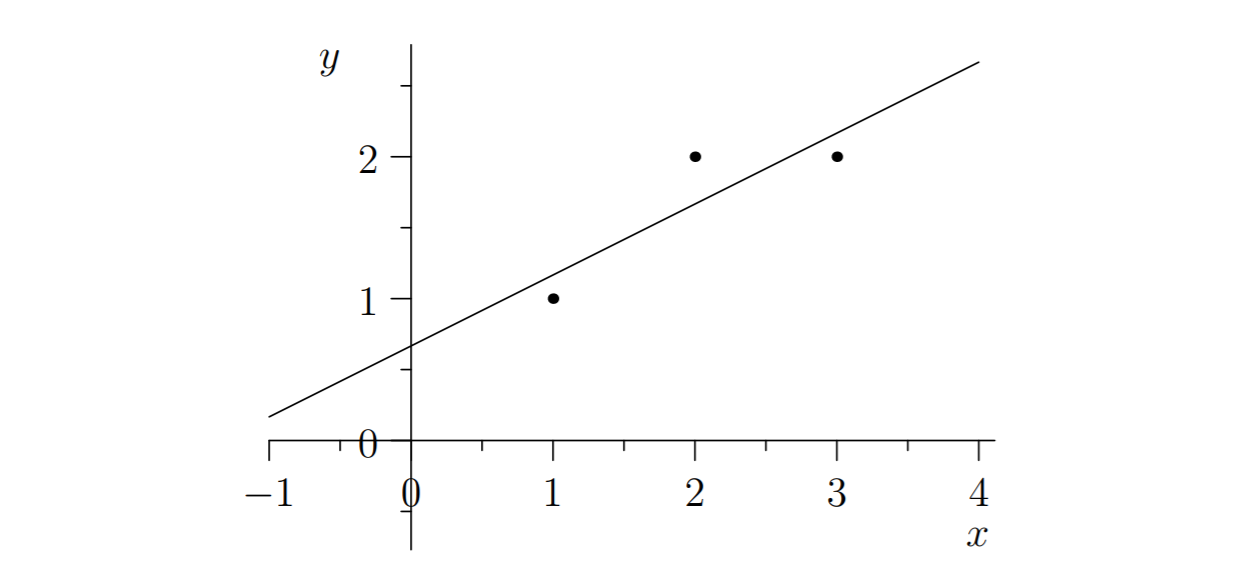
根据以上条件可以得到方程组 $\begin{cases} C+D&=1 \\ C+2D&=2 \\ C+3D&=2 \\ \end{cases}$，写作矩阵形式有 $\begin{bmatrix}1 &1 \\1 &2 \\1&3\\\end{bmatrix}\begin{bmatrix}C\\D\\\end{bmatrix}=\begin{bmatrix}1\\2\\2\\\end{bmatrix}$，也就是我们的 $Ax=b$，显然该方程组无解。

在寻求最优解之前，我们需要先定义总误差是什么，因为总误差能够衡量直线是否是更优的，定义了总误差我们才能通过最小化这个量，来找到最好的 $C$ 和 $D$（也即最优的直线）。

这里，我们定义误差为 $A\hat{x}-b=e$ 的模长的平方来作为误差，也即 $|A\hat{x}-b|^2=|e|^2=e_1^2+e_2^2+e_3^2$，我们要求其最小平方和（也即最小二乘）。

• 利用微积分的偏导来求最优解

  将误差展开用 $C$ 和 $D$ 的二元函数如下：

  $$\displaylines{ \begin{align} \|e\|^2&=e_1^2+e_2^2+e_3^2\\ &=(C+D-1)^2+(C+2D-2)^2+(C+3D-2)^2\\ &=3C^2+14D^2+9-10C-22D+12CD \end{align} }$$

  误差对 $C$ 求偏导为 $6C-10+12D=0$，说明单看 $C$ 的话，随着 $C$ 的增长，总误差的斜率先为负数后为正数，也即总误差先下降后上升。误差对 $D$ 求偏导为 $28D-22+12C=0$，说明单看 $D$ 的话，随着 $D$ 的增长，总误差的斜率先为负数后为正数，也即总误差先下降后上升。因此，总误差的驻点显然也即总误差的最小值（最优值）

  求解方程组 $\begin{cases}3C-5+6D=0\\14D-11+6C=0\end{cases}$ 得 $\hat{C}=\frac{2}{3},\hat{D}=\frac{1}{2}$，因此最优直线为 $y=\frac{2}{3}+\frac{1}{2}x$，代入 $x$ 可求得 $p_1=\frac{7}{6}, p_2=\frac{5}{3}, p_3=\frac{13}{6}$，自然 $e_1=-\frac{1}{6}, e_2=\frac{1}{3}, e_3=-\frac{1}{6}$。

  于是我们得到 $p=\begin{bmatrix}\frac{7}{6}\\\frac{5}{3}\\\frac{13}{6}\end{bmatrix}, e=\begin{bmatrix}-\frac{1}{6}\\\frac{1}{3}\\ -\frac{1}{6}\end{bmatrix}$，易看出 $b=p+e$，且 $p^Te=0$（也即 $p\bot e$）。

  $$\displaylines{ p^Te=\frac{7}{6}\cdot(-\frac{1}{6})+\frac{5}{3}\cdot\frac{1}{3}+\frac{13}{6}\cdot(-\frac{1}{6})=0\\ e^Ta_1=-\frac{1}{6}\cdot1+\frac{1}{3}\cdot1+(-\frac{1}{6})\cdot1=0\\ e^Ta_1=-\frac{1}{6}\cdot1+\frac{1}{3}\cdot2+(-\frac{1}{6})\cdot3=0\\ }$$

  综上可知，我们所求得的误差向量 $e$ 确实垂直于整个列空间，如 $\begin{bmatrix}1\\1\\1\end{bmatrix}, \begin{bmatrix}1\\2\\3\end{bmatrix}$（投影向量 $p$ 也在 $A$ 的列空间中）。

• 利用线性代数的投影来求最优解

  为了方便理解，我们需要再次搬出这张图：

  

  $A\hat{x}$ 也即 $A$ 的列空间中的向量，那么 $A\hat{x}-b$ 就表示了将列空间中的向量与 $b$ 相减，相减所得的向量，或许垂直于列空间，或许不垂直与列空间。

  但注意到，只有在相减所得的向量垂直于列空间的时候，$A\hat{x}-b$ 其模长的平方才最小，这也即让 $b$ 对列空间做投影，投影所得向量 $Pb$ 才是列空间中距离 $b$ 最近的向量。此时求解 $A\hat{x}=Pb$ 所得的 $\hat{x}$ 即为最优解！

  $$\displaylines{ A\hat{x}=Pb=A(A^TA)^{-1}A^Tb\\ 方程两边同乘以 A^T有：A^TA\hat{x}=A^TA(A^TA)^{-1}A^Tb=IA^Tb=A^Tb\\ 整理有：A^TA\hat{x}=A^Tb\\ 易得 A^TA= \begin{bmatrix}3&6\\6&14\end{bmatrix},\ A^Tb= \begin{bmatrix}5\\11\end{bmatrix}\\ \begin{bmatrix}3&6\\6&14\end{bmatrix} \begin{bmatrix}\hat C\\\hat D\end{bmatrix}= \begin{bmatrix}5\\11\end{bmatrix}\\ }$$

  写成方程组形式为 $\begin{cases}3\hat C+16\hat D&=5\\6\hat C+14\hat D&=11\\\end{cases}$，也称其为 $\color{red}{正规方程组（normal\ equations）}$。

  注意到该正规方程组正是先前求偏导所得的方程组。故所求得的结果也都是一样的：$\hat{C}=\frac{2}{3},\hat{D}=\frac{1}{2}$。

我们现在所做的运算实际上也称为 $\color{red}{线性回归（linear\ regression）}$。

此外，还需要补充说明一点，如果在上述例题中，还有另外一个点如 $(0, 100)$，那么最小二乘法就很容易被这个明显离群的值影响，通常使用最小二乘的时候要先去除掉明显离群的点！

---

标准正交向量组

有一种线性无关的情况是比较特殊的：互相垂直的各列一定是线性无关的。

更特殊地，我们会要求互相垂直的单位向量（标准正交），比如 $\left[\begin{array}{l}{1} \\ {0} \\ {0}\end{array}\right],\left[\begin{array}{l}{0} \\ {0} \\ {1}\end{array}\right],\left[\begin{array}{l}{0} \\ {1} \\ {0}\end{array}\right]$，这些向量所组成的向量组一般被称为标准正交向量组，标准正交向量组中的向量互相垂直（正交）且为单位向量（标准）！

同样的标准正交向量组还有：$\left[\begin{array}{c}{\cos \theta} \\ {\sin \theta }\end{array}\right],\left[\begin{array}{c}{-\sin \theta} \\ {\cos \theta}\end{array}\right]$。