Lec14 - 正交向量与子空间

第 14 课 正交向量与子空间

本章我们研究的重点还是之前提到过的子空间，但是本章我们主要从正交的角度来探讨这些子空间具有的性质，主要内容见下图。

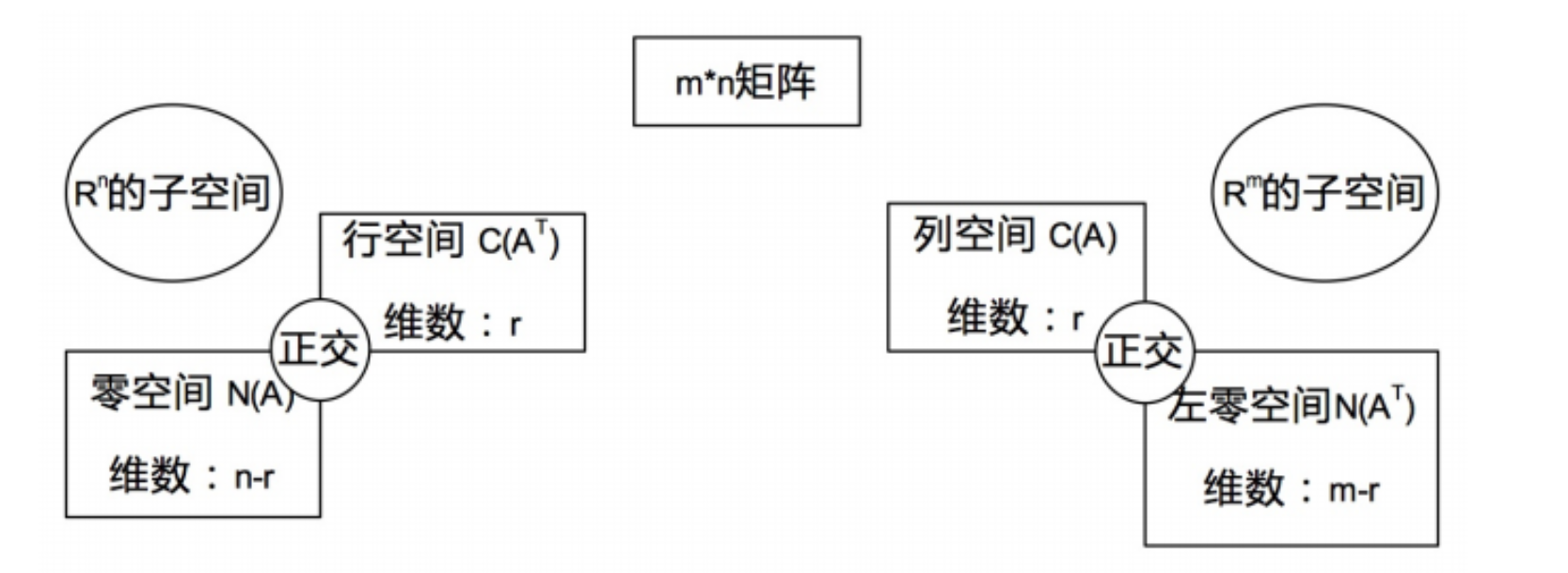
注意，上图指出了我们之前没有关注到的子空间的一些性质：对于一个矩阵，其零空间与行空间正交，其列空间与左零空间正交。

向量正交与空间正交

在线性代数中，正交就是垂直。无论我们讨论的是向量正交还是空间正交，都可以理解为垂直。

我们先研究最简单的向量正交：

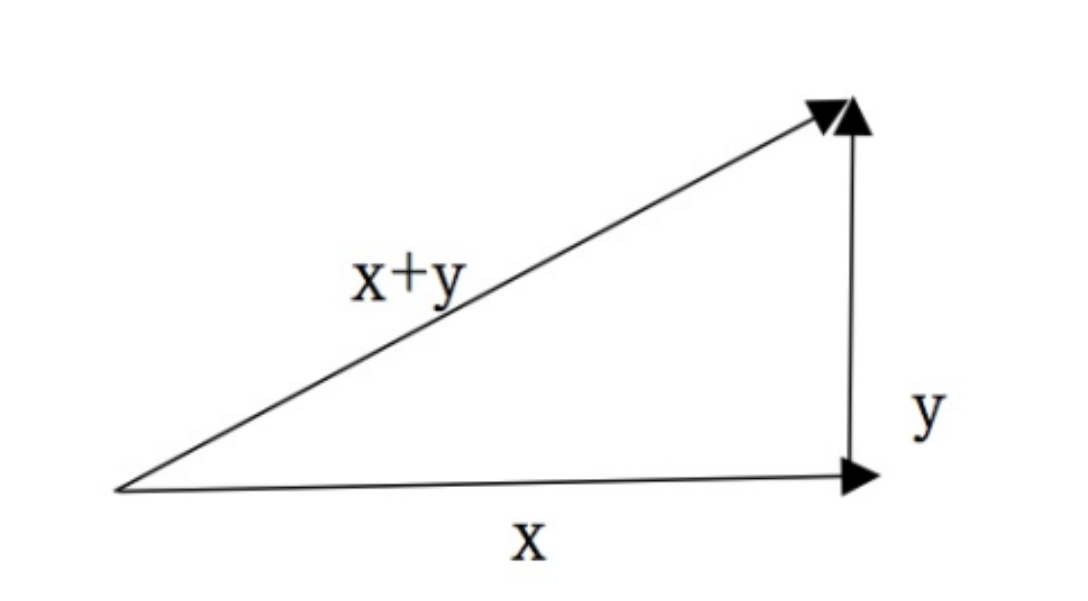
如上图，其中 $x$ 与 $y$ 向量之间相互垂直（正交）。根据垂直关系，可得 $x^Ty=0$，这是初高中的内容：如果两个向量相互垂直（正交），那么这两个向量的数量积（内积）为 $0$。

这个结论很漂亮，现在我们将证明这个结论。

$$\displaylines{ 根据勾股定律有： |x|^2+|y|^2=|x+y|^2 \ \\ 用向量来表示上式有：x^Tx+y^Ty=(x+y)^T(x+y)=(x^T+y^T)(x+y)\\ 化简得：0=x^Ty+y^Tx\\ \because x^Ty=y^Tx，都表示两个一维向量的数量积，所以可进一步化简得：2x^Ty=0\\ \therefore x^Ty=0 }$$

如果两个向量中其中一个是零向量，则两个向量一定正交。

接下来我们讨论空间正交，两个空间正交意味着：其中一个空间中的任意一个向量，都与另外一个空间中的任意一个向量正交。

这里需要注意一种容易混淆的情况，比如以黑板和地板为例，这两者所处的空间并非是空间正交的，最直接的反例是黑板平面和地板平面的交线处，这个交线处上的向量既属于黑板平面，也属于地板平面，最简单地，取交线处上的向量的平方存在不为 0 的可能，所以黑板平面与地板平面不是空间正交的。

这同时也提醒我们：两个平面若在非零向量处相交，则这两个平面一定是不正交的。

最后我们探究子空间中的正交情况，先简单地以 $R^2$ 的子空间为例，$R^2$ 的子空间有三种：整个平面 $D$，过原点的直线 $L$，零向量。

就这三个子空间而言，显然 $L$ 和 $D$ 是不可能正交的，因为 $L$ 就在平面 $D$ 上，但 $L$ 和零向量，$D$ 和零向量是正交的。此外， $L$ 和 $L$ 之间也可能是正交的：两条直线需要在原点处互相垂直。

---

矩阵的子空间的正交情况

一个矩阵，其零空间与行空间是正交的，它们之间的关系类似于将一个空间一分为二所得到的两个子空间。

我们先证明为什么零空间和行空间是正交的，而这一点很容易从 $Ax=0$ 上找到答案。

$$\displaylines{ Ax=\begin{bmatrix}row_1\ of\ A\\row_2\ of\ A\\...\\row_m\ of\ A\end{bmatrix}\begin{bmatrix}x_1\\x_2\\...\\x_n\end{bmatrix}=\begin{bmatrix}row_1\ of\ A\cdot x\\row_2\ of\ A\cdot x\\...\\row_m\ of\ A\cdot x\end{bmatrix}=\begin{bmatrix}0\\0\\...\\0\end{bmatrix} }$$

对于 $Ax=0$，有 $A$ 的每一行与 $x$ 相乘结果为零，这也即表明 $A$ 中的每一行与 $x$ 正交。$x$ 对应的是零空间中的任意向量，现 $A$ 中的每一行与 $x$ 相乘结果为零，那么显然 $A$ 中的行的线性组合与 $x$ 相乘结果依然为零，而 $A$ 中的行的线性组合对应的是行空间中的任意向量，所以，矩阵零空间与行空间正交。

同样地，根据 $A^Ty=0$，我们能以相同的方法证明矩阵的列空间和左零空间是正交的。

然后我们再回到之前所说的“它们之间的关系类似于将一个空间一分为二所得到的两个子空间”，这一点很重要，因为行空间和零空间的维数之和恰好为 $n$。举个例子：

$$\displaylines{ 设A=\begin{bmatrix}1&2&5\\2&4&10\end{bmatrix}\\ Ax=0可写为：\begin{bmatrix}1&2&5\\2&4&10\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=\begin{bmatrix}0\\0\\0\end{bmatrix} }$$

一眼就可以看出， $A$ 的秩为 $1$，所以其行空间的是 $1$ 维的，其零空间是 $2$ 维的（可以理解为垂直于向量 $\begin{bmatrix}1&2&5\end{bmatrix}^T$ 的一个平面），行空间维数与零空间维数相加为 $3$。而有意思的是行空间和零空间中的向量都是 $3$ 维的。

为了更加确切地讲述一分为二，我们引入正交补这个概念。称行空间和零空间是 $n$ 维空间里的正交补，是因为行空间和零空间正交且这两个子空间的维数之和为 $n$。举个简单的例子，三维空间中两条过原点的互相垂直的直线显然是相互正交的，但这两条直线对应的空间却不能被称为正交补，正交补的补就意味着，对于其中一个向量空间 $S$，另外一个向量空间 $T$ 则包含了所有垂直于 $S$ 的向量而不是部分。一分为二描述了一种彻底的程度。

---

无解方程 $Ax=b$ 的最优解

在上一课中我们看到了，矩阵的数据来源于实际测量，既然是测量，那么就存在测量不准确的情况，从而导致 $Ax=b$ 无解。此外，测量过程中极其细微的误差也可能导致无解。

除了测量因素以外，有时候 $A$ 是一个长方形矩阵，其行数 $m$ 很多，列数 $n$ 很少（也即较少的未知数要满足非常多的方程），这时候有些方程得到的结果可能是有很大误差的，这个误差来自 $b$，也即 $b$ 中有一部分是“坏数据”，这些“坏数据”使得方程无解。

我们可以不断去掉一些方程，用以剔除“坏数据”，最后得到一个可逆的方阵然后进行求解，但这种方法是不实际的，因为对于所有测量值而言，我们很难判断哪些是有效的好数据，哪些是无效的坏数据。一般我们希望利用所有的测量值求出“最优值”，类似于一种拟合。

一种常用的方法是在方程两侧乘以 $A^T$，无解方程从而改写成 $A^TA\hat{x}=A^Tb$，求解新方程的解 $\hat{x}$ 即为最优解。

注意，这个解 $\hat{x}$ 并非是 $Ax=b$ 的解，我们已经假设 $Ax=b$ 是无解的，也即符合方程的 $x$ 不存在。在已知 $Ax\ne b$ 的情况下，我们尝试求解 $A^TA\hat{x}=A^Tb$。

这种方法的原理我们将在下一章中进行详细的解析，彼时我们将明白为什么所得的解被称为“最优解”。

实际上，就算我们不懂原理，我们也大概能发现，乘以 $A^T$ 给方程带来了什么好的变化。乘以 $A^T$ 以后，我们得到矩阵 $A^TA$，这个矩阵是一个对称方阵，至少我们已经避免了长方矩阵的情况。一旦 $A^TA$ 是可逆的，那么解 $\hat{x}$ 就很容易求得了。

但实际上 $A^TA$ 未必是可逆的，当 $A$ 的各列线性相关的时候， $A^TA$ 就不可逆了。

为了证明这一点，我们需要给出两个性质（实际上只用第一个就够了）：

• 性质一：$N(A^TA)=N(A)$：$A^TA$ 与 $A$ 的零空间相同。

  $$\displaylines{ 证明：对于A^TAx=0，方程两边同乘以 x^T\\ 则有\ x^TA^TAx=(Ax)^TAx=0\\ \therefore Ax=0\\ \therefore 对于给定x，若A^TAx=0，那么有 Ax=0，反之亦然\\ \therefore A和 A^TA具有相同的零空间 }$$

• 性质二：$rank(A^TA)=rank(A)$：$A^TA$ 与 $A$ 的秩相同。

  这个结论的证明是简单的，利用已经证明的性质一可得：$dim(N(A^TA))=A^TA的列数-A^TA的秩=dim(N(A))=A的列数-A的秩$，又因为 $A^TA$ 和 $A$ 的列数相同，所以 $A^TA$ 与 $A$ 的秩相同。

显然，如果 $A$ 的各列线性相关，那么 $A$ 的零空间就存在非零向量使得 $A$ 的各列线性组合为零向量。因为 $A^TA$ 与 $A$ 的零空间相同，所以 $A^TA$ 的零空间就存在非零向量使得 $A^TA$ 的各列线性组合为零向量，既然存在这样的非零向量，那么 $A^TA$ 就不是一个可逆矩阵。