Lec12 - 图和网络
第 12 课 图和网络
本章着重于线性代数的应用。和前面的章节不同的是,本章中线性代数处理的矩阵都是有出处的,它们来自于实际问题,描述了问题的拓扑结构。应用数学中最重要的模型,离散数学称之为”图“。本章,我们将探索图和矩阵之间的联系(关联矩阵),从关联矩阵中推导出欧姆定律、基尔霍夫电流定律、欧拉公式,并探究这三者之间的关系。
为探究图和矩阵之间的联系,我们先给出一个有向图(如下),$4$ 个点($n=4$),$5$ 条边($m=5$)。
该有向图可以来自于一个电路系统,也可以来自于一个液压系统,甚至表示一个建筑结构,但在本课中我们将其视为一个电路网络。
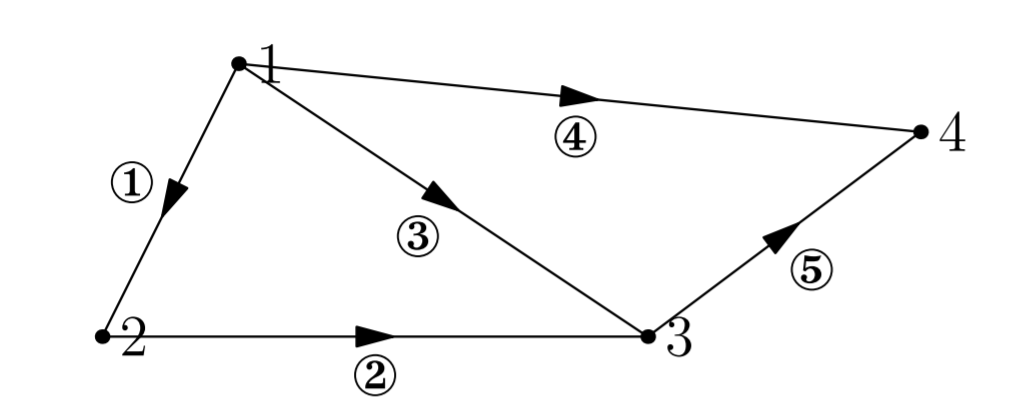
我们可以使用矩阵来表示一个图,矩阵中包含图中的所有信息。通过构造一个矩阵可以解析相应的图的含义,这样的矩阵叫做关联矩阵。在关联矩阵中,每一列代表一个节点,每一行代表一条边(行中的正负代表方向)。易得上(电路网络)图对应的关联矩阵 $A$ 如下:
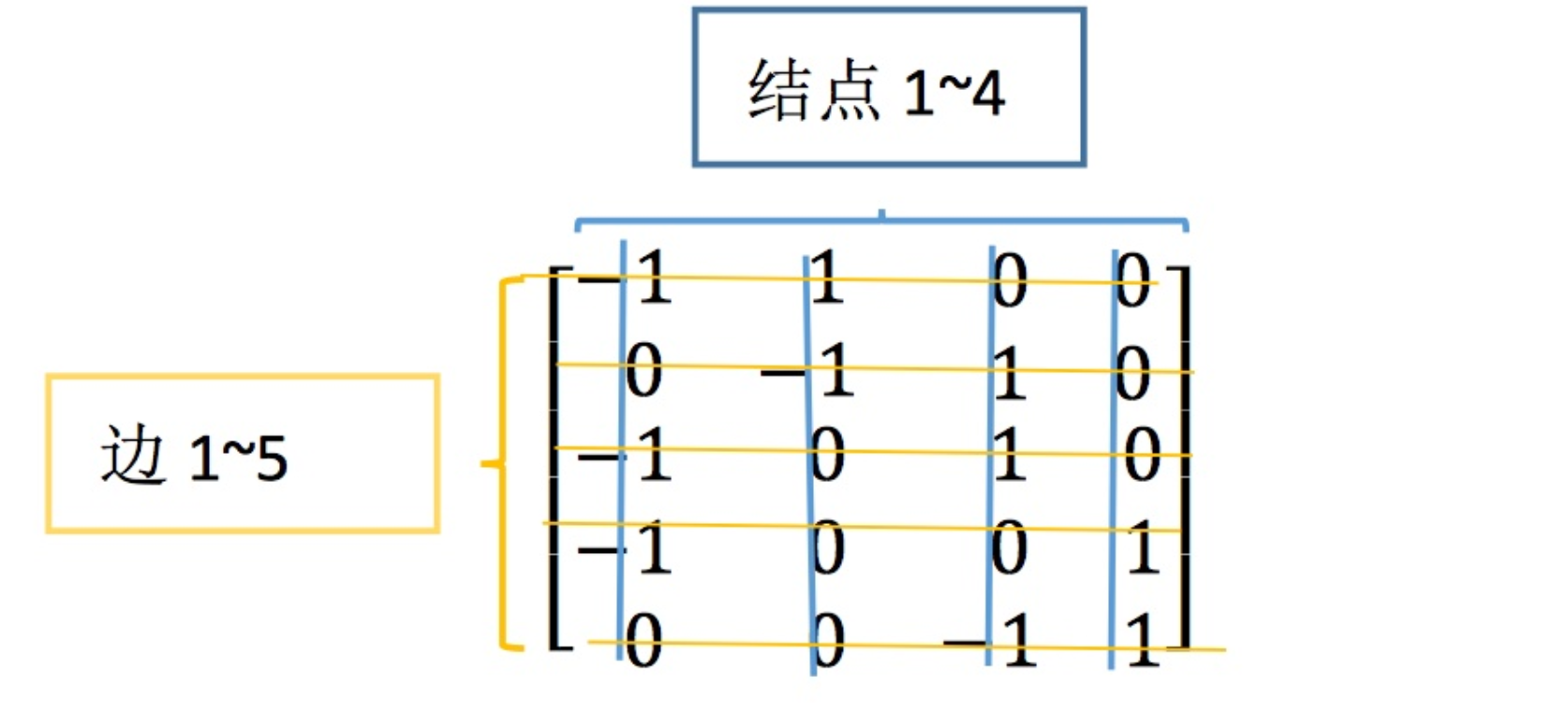
观察关联矩阵 $A$ 的第一行,第一行代表了电路网络图中边 $1$ 的情况,在图中,边 $1$ 以 点 $1$ 作为起点,以点 $2$ 作为终点,反映到矩阵上就是 $A_{(1,1)}=-1$,$A_{(1,2)}=1$,以此类推。
由图可知,边 $1$,边 $2$,边 $3$ 组成了一个回路,而观察矩阵可发现,这三条边对应的矩阵中的前三行是线性相关的,其中行 $1$ $+$ 行 $2$ $=$ 行 $3$ 。这说明“回路”意味着“相关”,回路对应的行向量组是线性相关的,这是一个图与矩阵之间很巧妙的联系。
关联矩阵源于问题,描述了问题的拓扑结构。一般来说关联矩阵是一个非常稀疏的矩阵,因为它的每行只有两个非零的元素,用于表示起点和终点。
我们已经从实际问题中抽象出相应的关联矩阵,现在我们试图去探究一些关于矩阵的主要问题。
矩阵 $A$ 的零空间是什么?
该问题等价于求解 $Ax=0$。
$Ax=0$ 的求解是简单的,但在给出答案之前,我们先引入上式的实际意义:将 $x=\begin{bmatrix}x_1&x_2&x_3&x_4\end{bmatrix}^T$ 视为各结点的电势,比如 $x_1$ 表示结点 $1$ 的电势。于是,上式中诸如 $x_2-x_1$ 的元素就相当于结点 $2$ 与结点 $1$ 这条边上的电势差。
容易得出解为 $x=c\begin{bmatrix}1&1&1&1\end{bmatrix}^T$,这也即等电势情况,当 $b=0$ 时, 每个结点上的电势都必须相等。
这代表了什么呢?
我们都知道,电势差和电流的形成之间有着直接关系,$b=0$ ,说明我们求解的情况是各个边上都没有电流(或者说电势差)的情况,而我们最后所得到的解就意味着,当各点电势相等时,边上电流(电势差)为零,符合我们的常识。 而这就是零空间的物理意义。
矩阵 $A$ 的左零空间是什么?
该问题等价于求解 $A^Ty=0$。
求解前我们先引入上式中 $y$ 的实际意义:将 $y=\begin{bmatrix}y_1&y_2&y_3&y_4&y_5\end{bmatrix}^T$ 视为各边上的电流。已知,电流和电势差的关系服从欧姆定律:边上的电流值是边上电势差的倍数,这个倍速就是边的电导即电阻的倒数,通常我们把这个常数视为一个系数矩阵记为 $C$。于是:
然后我们观察 $A^Ty=0$ 中的方程,比如第一个方程 $-y_1-y_3-y_4=0$,这个方程是关于结点 $1$ 上的电流的,方程指出结点 $1$ 上的电流之和为零。
实际上, $A^Ty=0$ 阐述了基尔霍夫电流定律(Kirchoff’s Current Law,简称 KCL),基尔霍夫电流定律是一个平衡方程,守恒定律,它说明了流入等于流出,电荷在结点上不会积累。
现在,我们开始求解 $y$。对 $A$ 进行消元可知 $A$ 的秩 $r$ 为 $3$。所以 $A$ 的左零空间的维数为 $m-r=5-3=2$,这也即左零空间的基有两个向量。在这里我们不打算使用前面讲过的方法来求解左零空间的基向量,而是直接通过观察求解以发现一些有趣的事情。
假设 $y_1=1$,也即 $1A$ 的电流在边 $1$ 上流动,那么由图(或者方程)可知 $y_2=1$。为符合基尔霍夫电流定律,那么只需再令 $y_3=-1$ ,也即让 $1A$ 的电流从结点 $2$ 流回结点 $1$,此时令 $y_4=y_5=0$,即可得到一个符合 KCL 的向量 $\begin{bmatrix}1&1&-1&0&0\end{bmatrix}^T$。容易发现,该解发生在结点 $1\rightarrow2\rightarrow3$ 组成的回路中。
同理,我们也容易得到发生在结点 $1\rightarrow3\rightarrow4$ 组成的回路中的解 $\begin{bmatrix}0&0&1&-1&1\end{bmatrix}^T$,该解显然也符合 KCL。
注意到,这两个从最小回路得到的向量彼此线性无关,这两个向量所组成的向量组恰好就是 $A$ 的左零空间的基。显然,我们似乎找到了一种捷径去求解关联矩阵的左零空间:借助图中的最小回路可以快速求得左零空间的基(注意是最小回路,这样可以确保每个回路所得出的向量之间都是线性无关的,故我们也称线性无关的回路)。事实上,图中的最小回路数 = $dim(N(A^T))$ = $m-r$。
最后,我们把视角放到结点 $1\rightarrow2\rightarrow3\rightarrow4$ 组成的大回路上,得到符合 KCL 的向量 $\begin{bmatrix}1&1&0&-1&1\end{bmatrix}^T$,恰为上述两个基向量之和。
矩阵 $A$ 的行空间是什么?这也即求 $A^T$ 的列空间。
在上文求 $A$ 的左零空间时,我们已经知道 $A$ 的秩 $r=3$,所以 $A^T$ 的秩也为 $3$。对 $A^T$ 消元可知,其列 $1,2,4$ 为主列。而在电路图中,这三列对应的三条边恰好是没有回路的,同时注意到列 $1,2,3$ 线性相关,在电路图中,这三列对应的三条边存在回路,于是可知,线性相关/无关性与回路有关,线性相关等价于存在回路,线性无关等价于没有回路。一般,我们把没有回路的图称为树。
通过探究矩阵 $A$ 的行空间,我们发现 $A^T$ 的秩与图存在的联系:矩阵的秩为 $r$ ,则图中有 $r$ 个线性无关的边,转换成图的语言那就是图中的 $r$ 个边构成了该图的最大无回路(存在回路就线性相关)。这里需要思考最大无回路的概念,就连通图而言,如果该图存在 $n$ 个结点,那么该图的最大无回路应该包括了 $n-1$ 条边,这条性质是很自然的,因为只要再多一条边,那么就会构成回路,从而线性相关。于是,我们可以得到,矩阵的秩 $r$ = 图中的结点数 $n$ 再减去 $1$。
万事具备,现在我们可以引出欧拉公式了。已知:
其中 $\#loops$ 为最小回路数,也即线性无关的回路数,$\#edges$ 为边数,$\#nodes$ 为结点数,将 (2) (3) (4) 代入到 (1) 中可得 $\#loops=\#edges-(\#nodes-1)$,再整理即:
这也即欧拉公式:$结点数 - 边数 + 最小回路 = 1$
综上内容,我们画出应用数学的基本方程的蓝图:
上述三式是在无外部电源情况下的方程。
考虑添加外部电源的因素,那么电源可以通过在边上加电压源和在点上加电流源两种方式接入。
如果是在边上加电压源,那么会直接体现在 $e=Ax$ 的 $e$ 中(边上两点的电势差改变了,$e$ 中的分量会因此改变)。如果是在点上加电流源,那么会直接体现在 $A^Ty=f$ 的 $f$ 中(点上的电流情况改变了,$f$ 中的分量会因此改变)。
联立上述三个等式可得 $A^TCAx=f$。需要注明的是,该方程作为一个平衡方程仅描述平衡状态,并没有考虑时间,牛顿定律不适用于此。